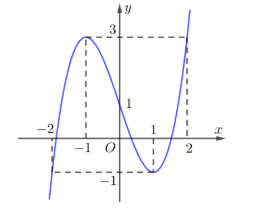
Cho hàm số bậc ba \[y = f\left( x \right)\] có đồ thị như hình vẽ:
a) [NB] Hàm số \[f\left( x \right)\] nghịch biến trên khoảng \[\left( { - 1;1} \right)\].
Đúng
Sai
b) [TH] Trên đoạn \[\left[ { - 2;2} \right]\], hàm số \[f\left( x \right)\] đạt giá trị lớn nhất bằng 2.
Đúng
Sai
c) [TH] Hàm số \[f\left( x \right)\] có hai điểm cực trị.
Đúng
Sai
d) [VD,VDC] \[f\left( x \right) = {x^3} - 3x + 1\].
Đúng
Sai
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) [NB] Do trên khoảng \[\left( { - 1;1} \right)\], đồ thị hàm số \[f\left( x \right)\] có hướng đi “xuống” suy ra hàm số \[f\left( x \right)\] nghịch biến trên khoảng \[\left( { - 1;1} \right)\]. Mệnh đề đúng.
b) [TH] Trên đoạn \[\left[ { - 2;2} \right]\], hàm số \[f\left( x \right)\] đạt giá trị lớn nhất bằng 3 tại \[x = - 1\] hoặc \[x = 2\]. Do đó mệnh đề sai.
c) [TH] Hàm số \[f\left( x \right)\] có hai điểm cực trị là \[x = - 1\] và \[x = 1\]. Mệnh đề đúng.
d) [VD,VDC] Do đồ thị hàm số đi qua điểm \[\left( {0;1} \right)\], suy ra \[f\left( x \right) = a{x^3} + b{x^2} + cx + 1\]
Mặt khác đồ thị hàm số đi qua các điểm có tọa độ là \[A\left( { - 1;2} \right),\,B\left( {1; - 1} \right),\,C\,\left( {2;2} \right)\]. Ta có hệ phương trình \[\left\{ \begin{array}{l}a{\left( { - 1} \right)^3} + b{\left( { - 1} \right)^2} + c\left( { - 1} \right) + 1 = 2\\a{\left( 1 \right)^3} + b{\left( 1 \right)^2} + c\left( 1 \right) + 1 = - 1\\a{\left( 2 \right)^3} + b{\left( 2 \right)^2} + c\left( 2 \right) + 1 = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - a + b - c = 1\\a + b + c = - 2\\8a + 4b + 2c = 1\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\\c = - 3\end{array} \right. \Rightarrow f\left( x \right) = {x^3} - 3x + 1\]
Vậy mệnh đề đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 1800.
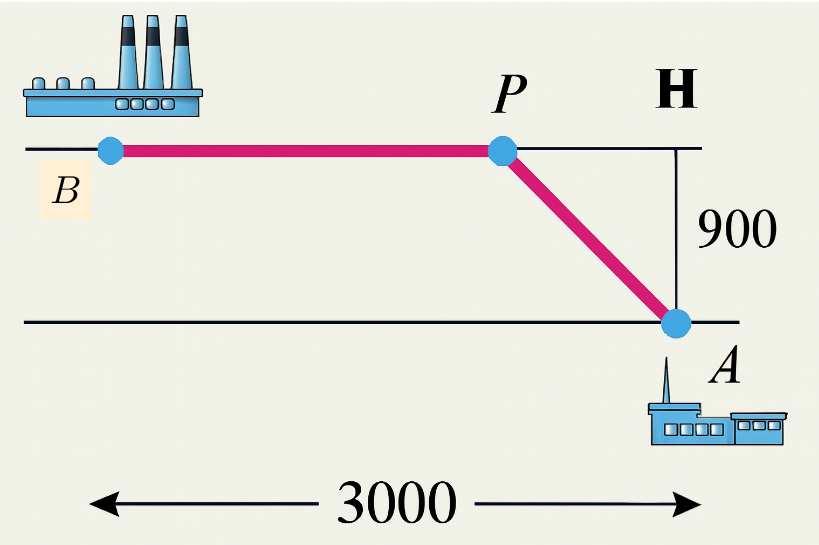
Đặt \(PH = x\,\,\left( {0 \le x \le 3000} \right)\)\( \Rightarrow \)\(PA = \sqrt {{x^2} + {{900}^2}} ;\,\,BP = 3000 - x\).
Do tỉ lệ giữa chi phí để kéo \(1\) mét cáp dưới nước và chi phí kéo \(1\) mét cáp trên bờ bằng \(1,25\)nên tổng chi phí đường cáp điện được kéo từ một trạm điện \(A\) đến một nhà máy \(B\) là
\(f\left( x \right) = PA.1,25 + PB = \sqrt {{x^2} + {{900}^2}} .1,25 + 3000 - x\) với \(0 \le x \le 3000\).
Ta có \(f'\left( x \right) = 1,25.\frac{x}{{\sqrt {{x^2} + {{900}^2}} }} - 1 = \frac{{1,25x - \sqrt {{x^2} + {{900}^2}} }}{{\sqrt {{x^2} + {{900}^2}} }}\).
\(f'\left( x \right) = 0 \Leftrightarrow \sqrt {{x^2} + {{900}^2}} = 1,25x \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} + {900^2} = 1,5625{x^2}\end{array} \right. \Leftrightarrow x = 1200\).
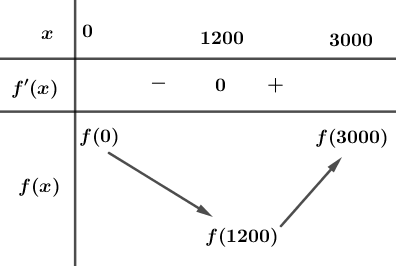
Vậy để tiết kiệm chi phí nhất thì vị trí \(P\) cách nhà máy \(B\) một đoạn bằng \(3000 - 1200 = 1800\,\,\,m\)
Lời giải
Đáp án: 63.
Chi phí vật liệu khi được chiết khấu: \(C\left( x \right) = \left( {1 - 5\% } \right)H\left( x \right) = 47,5{x^2} + 1900x + 47500\) đồng.
Lợi nhuận: \(L\left( x \right) = F\left( x \right) - xG\left( x \right) - C\left( x \right) = - 48,5{x^2} + 6100x - \frac{{100000x}}{{2x + 5}} + 52500\) với \(x \in \left[ {0,400} \right]\)
\( \Rightarrow L'\left( x \right) = - 97x + 6100 + \frac{{500000}}{{{{\left( {2x + 5} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x \simeq - 6,8\\x \simeq 2,1\\x \simeq 62,58\end{array} \right.\).
\(L\left( 0 \right) = 52500,L\left( {2,1} \right) \simeq 42270,L\left( {62,58} \right) \simeq 196220,28,L\left( {400} \right) = - 531789\)
\( \Rightarrow MaxL\left( x \right) = L\left( {62,58} \right) = 196220,28\) khi \(x \simeq 62,8 \simeq 63\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) [NB] Trong khoảng thời gian \[8\] giây kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của xe là \[26\left( {m/s} \right)\].
Đúng
Sai
b) [TH] Vận tốc của xe tại thời điểm \[t = 3\left( s \right)\] là \[21\left( {m/s} \right)\].
Đúng
Sai
c) [TH] Quãng đường mà xe đi được trong \[8\] giây đầu tiên (làm tròn đến hàng đơn vị) là \[157\left( m \right)\].
Đúng
Sai
d) [VD, VDC] Trong thời gian từ \[0 \le t \le 10\] giây, có thời điểm xe dừng lại.
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập