khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Phòng luyện thi Tốt nghiệp THPT
  3. Toán

Câu hỏi:

29/12/2025 3,578 Lưu

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)

Một xưởng in có \(13\) máy in được cài đặt tự động và được giám sát bởi một kỹ sư, mỗi máy in có thể in được \(12\) ấn phẩm/giờ. Chi phí cài đặt và bảo dưỡng cho mỗi máy in cho một đợt hàng là \(48000\) đồng. Chi phí trả cho kỹ sư giám sát là \(28000\) đồng/giờ. Đợt hàng này xưởng in nhận \(2280\) ấn phẩm. Gọi \(x\) là số lượng máy in cần sử dụng. Khi đó:

a) Chi phí cài đặt và bảo dưỡng cho đợt hàng là \(48x\) nghìn đồng.
Đúng
Sai
b) Số lượng ấn phẩm in được trong một giờ là \(12x\) ấn phẩm.
Đúng
Sai
c) Thời gian để in xong 2280 ấn phẩm là \(\frac{{190}}{x}\) giờ.
Đúng
Sai
d) Số máy cần sử dụng để tổng chi phí nhỏ nhất là \(10\) máy.
Đúng
Sai
Xem lời giải

Câu hỏi trong đề: Đề thi thử Toán Tốt nghiệp THPT 2025-2026 Bắc Ninh !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

a) Đúng.

Chi phí cài đặt và bảo dưỡng cho đợt hàng là \(48x\) nghìn đồng.

b) Đúng.

Số lượng ấn phẩm in được trong một giờ là \(12x\) ấn phẩm.

c) Đúng.

Thời gian để in xong 2280 ấn phẩm là \(\frac{{2280}}{{12x}} = \frac{{190}}{x}\) giờ.

d) Sai.

Chi phí cần để in \(2280\) ấn phẩm: \(C\left( x \right) = 28 \times \frac{{190}}{x} + 48x = \frac{{5320}}{x} + 48x\) (nghìn đồng, \(1 \le x \le 13\)).

Xét trên đoạn \(\left[ {1;13} \right]\): \(C'\left( x \right) =  - \frac{{5320}}{{{x^2}}} + 48 = 0 \Rightarrow x = \frac{{\sqrt {3990} }}{6}\).

Bảng biến thiên:

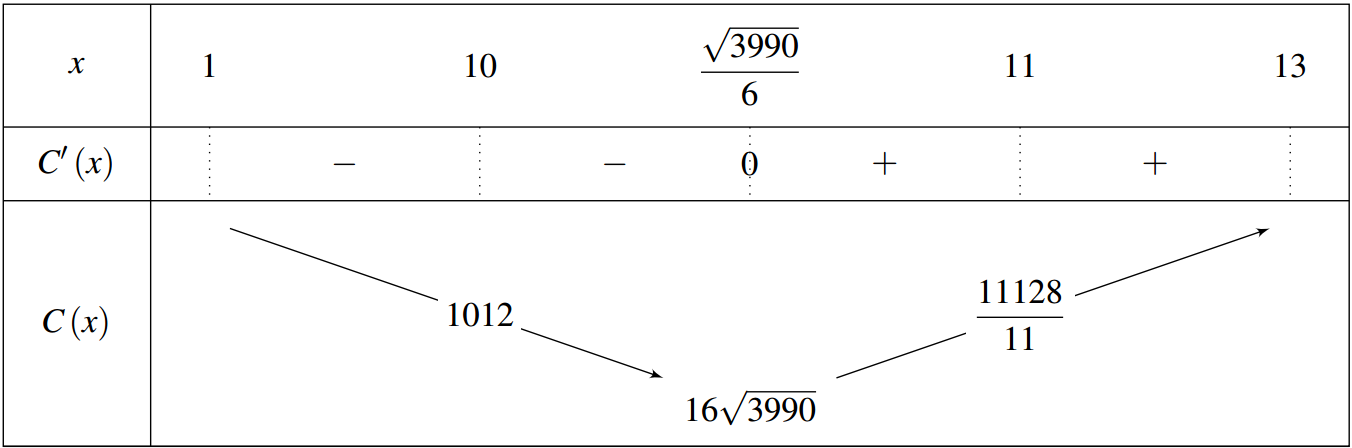
Vậy chi phí nhỏ nhất là \(\frac{{11128} (ảnh 1)

Vậy chi phí nhỏ nhất là \(\frac{{11128}}{{11}} \approx 1011,\left( {63} \right)\) nghìn đồng khi sử dụng \(11\) máy in.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chóp \[S.ABCD\] có đáy là hình thoi cạnh bằng \[1\], \[\widehat {BAD} = 60^\circ \], \[SA = 1\] và \[SA\] vuông góc với mặt đáy. Tính khoảng cách từ \[B\] đến mặt phẳng \[\left( {SCD} \right)\]? ( Kết quả làm tròn đến hàng phần trăm).

Lời giải

Đáp án:

0,65

Lời giải

Đáp án: \[0,65\].

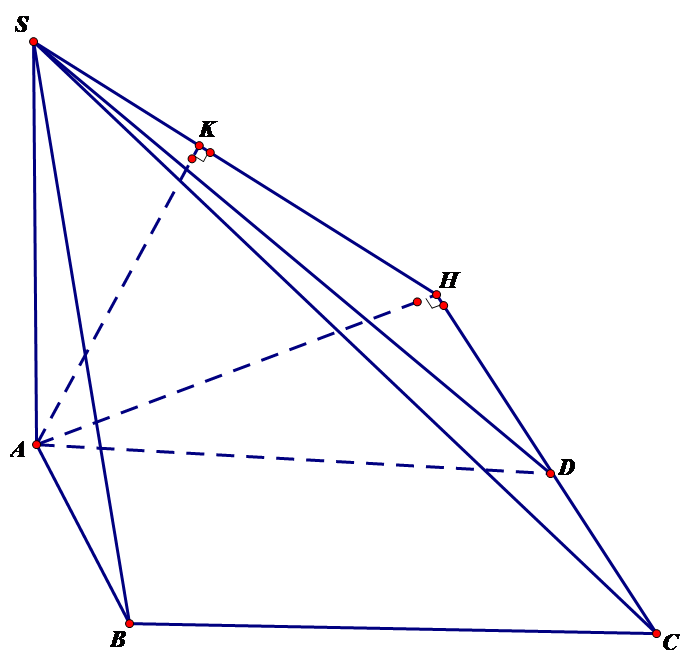
Vậy \[d\left( {B,\left( {S (ảnh 1)

Kẻ \[AH \bot CD\] tại \[H\], \[AK \bot SH\] tại \[K\]

Vì \[AH \bot CD\] và \[AS \bot CD\] nên \[CD \bot \left( {SAH} \right)\]\[ \Rightarrow AK \bot CD\] mà \[AK \bot SH\] nên \[AK \bot \left( {SCD} \right)\]

Vậy \[d\left( {A,\left( {SCD} \right)} \right) = AK\].\[\widehat {ADH} = \widehat {BAD} = 60^\circ \] (so le trong).

\[AH = AD.\sin 60^\circ  = \frac{{\sqrt 3 }}{2},AK = \frac{{SA.AH}}{{\sqrt {S{A^2} + A{H^2}} }} = \frac{{\sqrt {21} }}{7} \approx 0,65\].

Vậy \[d\left( {B,\left( {SCD} \right)} \right) \approx 0,65.\] (vì \[AB//\left( {SCD} \right)\]).

Câu 2

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Một mặt bằng đường đua được mô hình hoá bởi một hình bao gồm hai cạnh của một hình chữ nhật và hai nửa đường tròn bằng nhau. Một khán giả đang ngồi xem đua tại vị trí điểm \[P\](với các thông số được cho như hình vẽ). Gọi \[Q\] là điểm trên đường đua sao cho khoảng cách từ \[P\] đến \[Q\] là ngắn nhất. Khoảng cách ngắn nhất đó bằng bao nhiêu kilomet?

Một mặt bằng đường đua được mô hình hoá bởi một hình bao gồm hai cạnh của một hình chữ nhật và hai nửa đường tròn bằng nhau. Một khán giả đang ngồi xem đua tại vị trí điểm \[P\](với các thông số được cho như hình vẽ). (ảnh 1)

Lời giải

Đáp án:

1,5

Đáp án: \[1,5\].

Một mặt bằng đường đua được mô hình hoá bởi một hình bao gồm hai cạnh của một hình chữ nhật và hai nửa đường tròn bằng nhau. Một khán giả đang ngồi xem đua tại vị trí điểm \[P\](với các thông số được cho như hình vẽ). (ảnh 2)

Gọi \[O\] là tâm đường tròn \[(R = 1)\]; \[K\] là điểm giữa đường tròn và đường thẳng; \[H\] là hình chiếu của \[P\] lên \[OK\]. Có \[PH = 2\;km\]; \[OH = OK + KH = 1 + 0,5 = 1,5\;km\]; \[OP = \sqrt {{2^2} + 1,{5^2}}  = 2,5\;km\].

Dễ thấy vị trí \[Q\] để cho \[PQ\] ngắn nhất là \[P,Q,O\] thẳng hàng.

Khi đó \[\min PQ = OP - R = 2,5 - 1 = 1,5\;km\].

Câu 3

Một lớp 11 của một trường THPT có \[18\] học sinh học giỏi môn Toán, \[12\] học sinh học giỏi môn Ngữ Văn và có \[10\] học sinh không giỏi môn nào (lớp không có học sinh học giỏi môn khác ngoài 2 môn Toán và Ngữ Văn). Dịp đại hội Đoàn xã tháng 10 vừa qua, lớp này được chọn ra \[2\] học sinh giỏi để dự đại hội Đoàn. Xác suất để trong \[2\] học sinh được chọn có đúng \[1\] học sinh giỏi cả Toán và Ngữ văn là \(\frac{9}{{23}}.\) Số học sinh của lớp 11 này bằng bao nhiêu?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong không gian với hệ tọa độ \[Oxyz\], cho \(\Delta ABC\)với \(A\left( {1; - 3;3} \right),B\left( {2; - 4;5} \right),C\left( {3; - 2;1} \right)\)
a) \(\overrightarrow {AB} = \left( { - 1;1; - 2} \right).\)
Đúng
Sai
b) Điểm \(G\left( {a;b;c} \right)\) là trọng tâm của tam giác \(\Delta ABC\) thì \(a + b + c = 2\).
Đúng
Sai
c) Điểm \(I\left( {x;y;z} \right)\)thỏa mãn \(2\overrightarrow {IA} + \overrightarrow {IB} + 3\overrightarrow {IC} = \vec 0,\) khi đó \(2x + y + z = 4.\)
Đúng
Sai
d) Gọi \(M\left( {x;y;z} \right)\) là điểm trên mặt phẳng tọa độ \(\left( {Oyz} \right)\)sao cho biểu thức \[P = - 2M{A^2} - M{B^2} - 3M{C^2}\] đạt giá trị lớn nhất. Khi đó \(x + y - z < - 5\).
Đúng
Sai

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Có 10 người đang đứng đợi tàu ở sân ga. Nhà ga thông báo đoàn tàu mang số hiệu QH15 đang tiến vào sân ga chỉ còn 4 toa hành khách có thể lên tàu, mỗi toa tàu trong số 4 toa này đều có thể chứa thêm tối đa 10 hành khách. Để lên tàu hành khách đang đứng đợi tàu ở sân ga cần chọn một trong các cửa ga mang số 1, 2, 3, 4, xếp thành một hàng dọc ở trước đó, khi tàu dừng hẳn từ các cửa ga 1, 2, 3, 4 hành khách đã xếp hàng lần lượt theo thứ tự từ đầu hàng đến cuối hàng bước lên tàu. Gọi T là số cách 10 hành khách đang đứng đợi tàu ở sân ga lên tàu QH15, biết rằng mỗi toa tàu đều phải có ít nhất một khách lên tàu. Giá trị của \(\frac{T}{{76800}}\) bằng bao nhiêu?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số \(f(x) = {3^x} \cdot \ln x\)
a) Tập xác định của hàm số đã cho \(D = \mathbb{R}\).
Đúng
Sai
b) \(f'(x) = {3^x}\left( {\ln x + \frac{1}{x}} \right)\)
Đúng
Sai
c) Hàm số đã cho đồng biến trên \((3; + \infty )\).
Đúng
Sai
d) Có \(18\) số nguyên \(x\) sao cho ứng với mỗi số nguyên \(x\) có đúng 3 số nguyên \(y\) thỏa mãn bất phương trình: \({3^{{y^2} - \frac{{|x|}}{x}}} \le {\log _{{y^2} + 3}}\left( {\frac{{|x|}}{3} + 3} \right)\).
Đúng
Sai

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập