Trong không gian, cho mặt cầu \(\left( S \right)\) có phương trình: \({(x - 1)^2} + {(y - 2)^2} + {(z - 1)^2} = 9\), đồng thời điểm \(M\) có toạ độ \(M\left( {9;3;5} \right)\). Gọi \(I\) là tâm của mặt cầu \(\left( S \right),N\) là điểm nằm trên mặt cầu \(\left( S \right)\) sao cho \(N,I,M\) không thẳng hàng, \(A\) là điểm có tọa độ \(\left( { - \frac{{37}}{9};\frac{{ - 44}}{9};\frac{{67}}{9}} \right)\). \(K\) là điểm sao cho \(\overrightarrow {IM} = 9\overrightarrow {IK} \). Giá trị nhỏ nhất của biểu thức \(T = MN + 3NA\) là:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là B
Phương pháp giải
Sử dụng điểm trung gian.
Lời giải
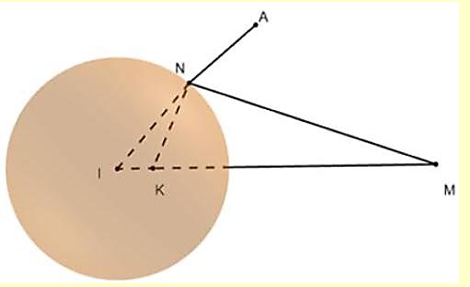
Tính được \(IM = 9 = 3R\).
Gọi \(K\) là điểm sao cho \(\overrightarrow {IM} = 9\overrightarrow {IK} \).
Có \(\overrightarrow {IM} \left( {8;1;4} \right) \Rightarrow \overrightarrow {IK} \left( {\frac{8}{9};\frac{1}{9};\frac{4}{9}} \right) \Rightarrow K\left( {\frac{{17}}{9};\frac{{19}}{9};\frac{{13}}{9}} \right)\).
Xét 2 tam giác \(IKN\) và \(INM\) có:
\(\left\{ {\begin{array}{*{20}{l}}{\frac{{IK}}{{IN}} = \frac{{IN}}{{IM}} = \frac{1}{3}}\\{\widehat {KIN} = \widehat {NIM}}\end{array} \Rightarrow } \right.\) hai tam giác \(IKN\) và \(INM\) đồng dạng.
Do hai tam giác \(IKN\) và \(INM\) đồng dạng nên \(\frac{{NM}}{{KN}} = \frac{{IN}}{{IK}} = 3 \Rightarrow NM = 3KN\)
Khi đó, \(T = 3\left( {KN + NA} \right) \ge 3KA = 3\sqrt {{{\left( {\frac{{17}}{9} + \frac{{37}}{9}} \right)}^2} + {{\left( {\frac{{19}}{9} + \frac{{44}}{9}} \right)}^2} + {{\left( {\frac{{13}}{9} - \frac{{67}}{9}} \right)}^2}} = 33\)
Vậy giá trị nhỏ nhất của biểu thức \(T\) là 33.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là C
Phương pháp giải
Vận dụng lí thuyết về dòng điện xoay chiều
Lời giải
Ta có: Trong 1 chu kỳ, dòng điện có giá trị tức thời bằng giá trị hiệu dụng của nó 2 lần
Vậy trong 50 chu kỳ, dòng điện có giá trị tức thời bằng giá trị hiệu dụng của nó 100 lần.
Câu 2
C. Tỉ lệ gia tăng dân số tự nhiên Bun-ga-ri cao hơn Cộng hòa Nam Phi.
Lời giải
Đáp án đúng là D
Phương pháp giải
Nhận xét bảng số liệu và công thức tính tỉ lệ gia tăng dân số.
Lời giải
- Tỉ lệ gia tăng dân số (%) = (Tỉ suất sinh – tỉ suất tử)/10
- Dựa vào công thức trên, ta tính được tỉ lệ gia tăng dân số của Cộng hòa Nam Phi năm 2020 là: (20,7 – 9,5)/10 = 1,12%.
- Tương tự như vậy, tỉ lệ gia tăng dân số của Ma-lai-xi-a; Bun-ga-ri và An-ba-ni lần lượt là 1,17%; 0,64%; 0,4%.
=> An-ba-ni là quốc gia có tỉ lệ gia tăng dân số tự nhiên thấp nhất là nhận xét đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập