Để chặn đường hành lang hình chữ L, người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ). Biết \[a = 24\] và \[b = 3\]. Hỏi cái sào thỏa mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu? (kết quả làm tròn đến hàng phần chục).
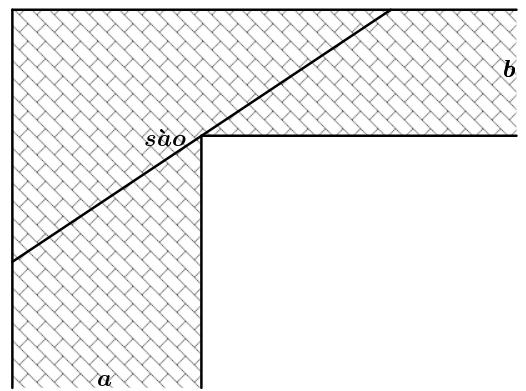
Để chặn đường hành lang hình chữ L, người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ). Biết \[a = 24\] và \[b = 3\]. Hỏi cái sào thỏa mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu? (kết quả làm tròn đến hàng phần chục).

Quảng cáo
Trả lời:
Đáp án:
Đáp án: 33,5
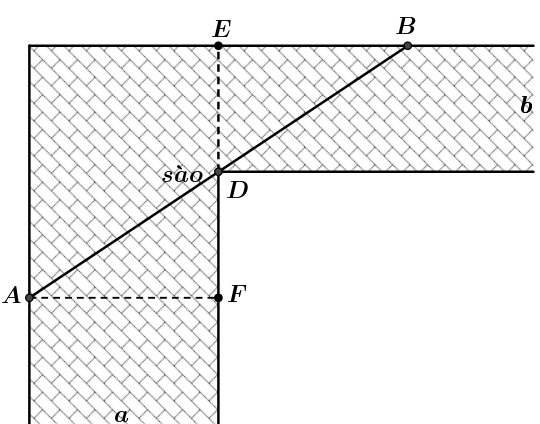
Đặt các điểm như hình vẽ.
Đặt \(DF = x\), \(x > 0\), ta có \(\Delta ADF\) đồng dạng với \(\Delta BED\) nên \(\frac{{EB}}{{ED}} = \frac{{AF}}{{DF}}\)\( \Rightarrow EB = \frac{{ab}}{x}\)
Gọi \[l\] là chiều dài của que sào, ta có \({l^2} = A{B^2} = {\left( {x + b} \right)^2} + {\left( {a + \frac{{ab}}{x}} \right)^2} = f\left( x \right)\).
Đạo hàm:
\(f'\left( x \right) = 2\left( {x + b} \right) - 2\frac{{ab}}{{{x^2}}}\left( {a + \frac{{ab}}{x}} \right) = 2\left( {x + b} \right)\left( {1 - \frac{{{a^2}b}}{{{x^3}}}} \right)\); \(f'\left( x \right) = 0 \Leftrightarrow x = \sqrt[3]{{{a^2}b}} = 12\).
Dễ dàng suy ra được \(\min \,f\left( x \right) = f\left( {12} \right) = 1125\)
Vậy giá trị nhỏ nhất của que sào là \(l = \sqrt {1125} = 15\sqrt 5 \approx 33,5\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp số : 30
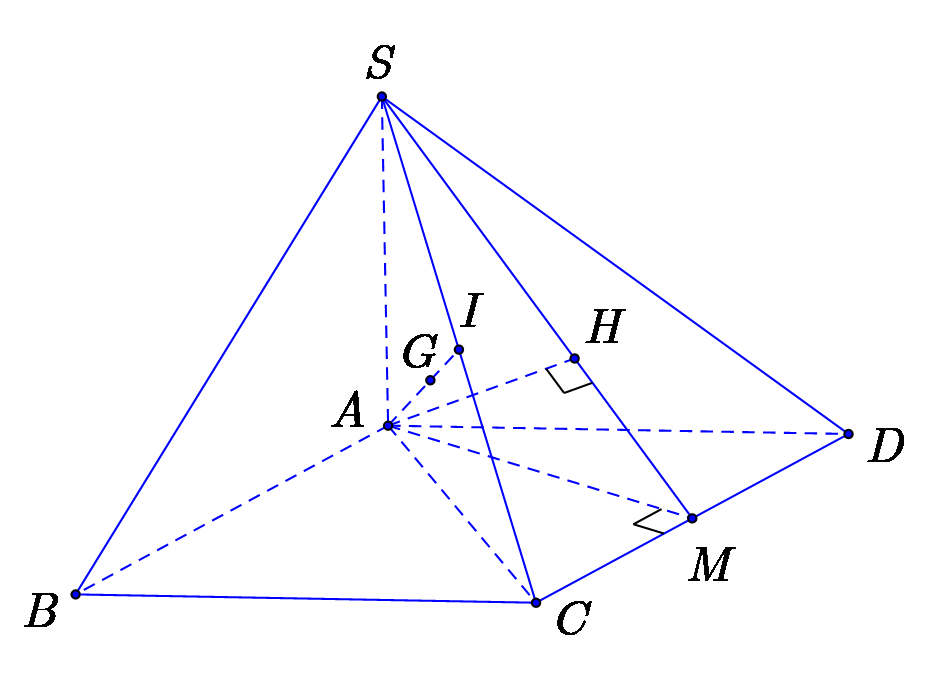
Gọi \(M,I\)lần lượt là trung điểm \(CD,\,SC\).
Theo giả thiết ta có tam giác \(ACD\) đều. Suy ra \(AM = \frac{{AD\sqrt 3 }}{2} = \frac{{\sqrt 3 a}}{2}\).
Kẻ \(AH \bot SM\,\,\left( {H \in SM} \right)\) thì \(AH \bot \left( {SCD} \right)\).
Ta có \(GI = \frac{1}{3}AI\) nên \(d\left( {G,\left( {SCD} \right)} \right) = \frac{1}{3}d\left( {A,\left( {SCD} \right)} \right) = \frac{1}{3}AH\)
\( = \frac{1}{3}.\frac{{AM.SA}}{{\sqrt {A{M^2} + S{A^2}} }} = \frac{1}{3}.\frac{{\frac{{\sqrt 3 a}}{2}.\sqrt 3 a}}{{\sqrt {\frac{{3{a^2}}}{4} + 3{a^2}} }} = \frac{{\sqrt {15} a}}{{15}}\)
Vậy \(d\left( {G,\left( {SCD} \right)} \right) = \frac{{\sqrt {15} a}}{{15}}\).
Lời giải
Đáp án: 34,1
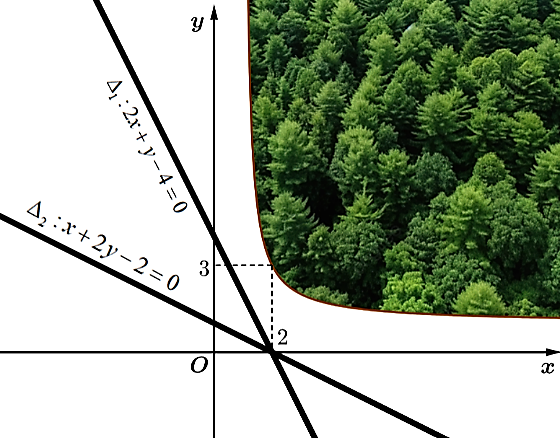
Đồ thị hàm số có tiệm cận đứng \(x = - b = 1 \Rightarrow b = - 1\).
Khi đó đồ thị hàm số \(y = \frac{{x + a}}{{x - 1}}\) qua \(\left( {2\,;\,\,3} \right) \Rightarrow 3 = \frac{{2 + a}}{{2 - 1}} \Rightarrow a = 1\); hàm số là (C).
Ta nhận thấy để khoảng cách từ điểm m thuộc khu vườn đến hai đường thẳng là nhỏ nhất thì điểm M phải thuộc đồ thị hàm số.
Gọi \(M\left( {{x_0}\,;\,\,\frac{{{x_0} + 1}}{{{x_0} - 1}}} \right) \in \left( C \right),\,\,{x_0} > 1\). Tổng khoảng cách từ M đến hai đường thẳng \({\Delta _1},\,\,{\Delta _2}\) là
\(d = d\left( {M\,,\,\,{\Delta _1}} \right) + d\left( {M\,,\,\,{\Delta _2}} \right) = \frac{{\left| {2{x_0} + \frac{{{x_0} + 1}}{{{x_0} - 1}} - 4} \right|}}{{\sqrt 5 }} + \frac{{\left| {{x_0} + 2 \cdot \frac{{{x_0} + 1}}{{{x_0} - 1}} - 2} \right|}}{{\sqrt 5 }}\) ;
\(\sqrt 5 d = \left| {\frac{{2x_0^2 - 5{x_0} + 5}}{{{x_0} - 1}}} \right| + \left| {\frac{{x_0^2 - {x_0} + 4}}{{{x_0} - 1}}} \right| = \frac{{2x_0^2 - 5{x_0} + 5}}{{{x_0} - 1}} + \frac{{x_0^2 - {x_0} + 4}}{{{x_0} - 1}}\)
(vì \(\left\{ \begin{array}{l}2x_0^2 - 5{x_0} + 5 > 0\\{x_0} - 1 > 0\\x_0^2 - {x_0} + 4 > 0\end{array} \right.\,,\,\,\forall {x_0} > 1\)).
Đặt \(\sqrt 5 d = \frac{{3x_0^2 - 6{x_0} + 9}}{{{x_0} - 1}} = g\left( x \right)\) với \(x > 1\).
Ta có: \(g'\left( x \right) = \frac{{3x_0^2 - 6{x_0} - 3}}{{{{\left( {{x_0} - 1} \right)}^2}}}\); \(g'\left( x \right) = 0 \Rightarrow 3x_0^2 - 6{x_0} - 3 = 0 \Rightarrow {x_0} = 1 + \sqrt 2 > 1\).
Ta có: .
Dấu đẳng thức xảy ra khi \({x_0} = 1 + \sqrt 2 \)\( \Rightarrow M\left( {1 + \sqrt 2 \,;\,\,1 + \sqrt 2 } \right)\).
Khoảng cách OM trên thực tế là mét.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Chọn D Dựa vào bảng biến thiên ta thấy: Hàm số đã cho đồng biến trên các khoảng \[\left( { - \infty \,;\, - 1} \right)\] và \(\left( {0\,;\,1} \right)\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/6-1766998416.png)