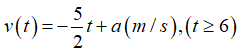Cho phương trình \({\rm{lo}}{{\rm{g}}_4}{(x + 1)^2} + 2 = {\rm{lo}}{{\rm{g}}_{\sqrt 2 }}\sqrt {4 - x} + {\rm{lo}}{{\rm{g}}_8}{(4 + x)^3}\). Tổng các nghiệm của phương trình là
Quảng cáo
Trả lời:
Đáp án đúng là C
Phương pháp giải
Giải phương trình logarit.
Lời giải
\(\left\{ {\begin{array}{*{20}{l}}{{{(x + 1)}^2} > 0}\\{4 - x > 0}\\{4 + x > 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne - 1}\\{ - 4 < x < 4}\end{array}} \right.} \right.\).
Ta có : \({\rm{lo}}{{\rm{g}}_4}{(x + 1)^2} + 2 = {\rm{lo}}{{\rm{g}}_{\sqrt 2 }}\sqrt {4 - x} + {\rm{lo}}{{\rm{g}}_8}{(4 + x)^3}\)
\( \Leftrightarrow {\rm{lo}}{{\rm{g}}_2}\left| {x + 1} \right| + {\rm{lo}}{{\rm{g}}_2}4 = {\rm{lo}}{{\rm{g}}_2}\left( {4 - x} \right) + {\rm{lo}}{{\rm{g}}_2}\left( {4 + x} \right)\)
\( \Leftrightarrow {\rm{lo}}{{\rm{g}}_2}4.\left| {x + 1} \right| = {\rm{lo}}{{\rm{g}}_2}\left( {16 - {x^2}} \right) \Leftrightarrow 4\left| {x + 1} \right| = 16 - {x^2}\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{4\left( {x + 1} \right) = 16 - {x^2}}\\{4\left( {x + 1} \right) = - \left( {16 - {x^2}} \right)}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} + 4x - 12 = 0}\\{{x^2} - 4x - 20 = 0}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2}\\{x = - 6}\\{x = 2 + 2\sqrt 6 }\\{x = 2 - 2\sqrt 6 }\end{array}} \right.\).
Kết hợp với điều kiện ta có 2 nghiệm thỏa mãn \(x = 2;x = 2 - 2\sqrt 6 \).
Vậy tổng các nghiệm là \(4 - 2\sqrt 6 \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là "2/3"
Phương pháp giải
Xác suất có điều kiện.
Lời giải
Gọi A là biến cố "người được chọn là nam"
Gọi \(B\) là biến cố "Người được chọn là người phải trực"
Khi đó ta có \(\overline A \) là biến cố "người được chọn là nữ", suy ra \[P\left( {\overline A } \right) = \frac{{30}}{{100}} = \frac{3}{{10}}\].
Là biến cố "người được chọn là nữ gần cơ quan", suy ra \(P\left( {B\overline A } \right) = \frac{{60 - 40}}{{100}} = \frac{2}{{10}}\).
Xác suất người được chọn là nữ và là người trực cơ quan là
\(P\left( {B\mid A} \right) = \frac{{P\left( {B\overline A } \right)}}{{P\left( {\overline A } \right)}} = \frac{{\frac{2}{{10}}}}{{\frac{3}{{10}}}} = \frac{2}{3}\).
Lời giải
Đáp án đúng là "10"
Phương pháp giải
Công thức tích phân.
Lời giải
Ta có \(v\left( 6 \right) = {v_0} \Leftrightarrow a = {v_0} + 15\) suy ra \(v\left( t \right) = \frac{{ - 5}}{2}t + {v_0} + 15\).
Gọi \(n\) là thời điểm vật dừng hẳn, khi đó ta có
\(v\left( n \right) = 0 \Leftrightarrow n = \frac{2}{5}\left( {{v_0} + 15} \right) \Leftrightarrow n = \frac{{2{v_0}}}{5} + 6\).
Khi đó ta có phương trình tổng quãng đường vật đi được là
\( \Leftrightarrow 80 = 6.{v_0} - \frac{5}{4}\left( {{n^2} - {6^2}} \right) + {v_0}\left( {n - 6} \right) + 15\left( {n - 6} \right)\)
\( \Leftrightarrow 80 = 6.{v_0} - \frac{5}{4}\left( {\frac{{4{{\left( {{v_0}} \right)}^2}}}{{25}} + \frac{{24{v_0}}}{{25}}} \right) + {v_0}\frac{{2{v_0}}}{5} + 15\frac{{2{v_0}}}{5}\)
\( \Leftrightarrow v_0^2 + 36{v_0} - 400 = 0 \Leftrightarrow {v_0} = 10\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.