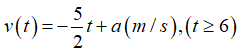Cho hình chóp đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\sqrt 2 \). Biết rằng bán kính mặt cầu ngoại tiếp hình chóp bằng \(\frac{{9\sqrt 2 }}{8}a\), độ dài cạnh bên lớn hơn độ dài cạnh đáy. Khoảng cách giữa hai đường thẳng \(AB\) và \(SD\) bằng:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là A
Phương pháp giải
Tìm khoảng cách giữa hai đường thẳng chéo nhau.
Lời giải
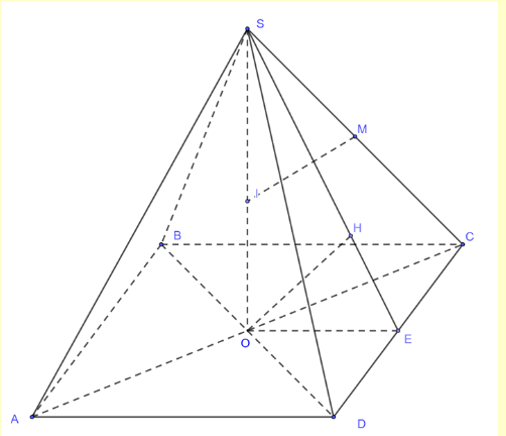
Gọi \(O = AC \cap BD,M\) là trung điểm của \(SC\).
Trong tam giác \(SAC\), dựng đường trung trực của đoạn thẳng \(SC\) tại \(I,I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABCD\) có bán kính \(R = SI = \frac{{9\sqrt 2 }}{8}a\).
Vi độ dài cạnh bên lớn hơn độ dài cạnh đáy nên tâm \(I\) của mặt cầu ngoại tiếp hình chóp thuộc đoạn \(SO\).
Ta gọi \(x\) là độ dài cạnh bên của hình chóp.
Ta dễ thấy \({\rm{\Delta }}SOC\) đồng dạng với \({\rm{\Delta }}SMI\).
Suy ra
\(\frac{{SI}}{{SC}} = \frac{{SM}}{{SO}} \Leftrightarrow \frac{{\frac{{9\sqrt 2 }}{8}a}}{x} = \frac{{\frac{x}{2}}}{{\sqrt {{x^2} - {a^2}} }} \Leftrightarrow 9a\sqrt {{x^2} - {a^2}} = 2\sqrt 2 {x^2} \Leftrightarrow 81{a^2}\left( {{x^2} - {a^2}} \right) = 8{a^4}\)
\( \Leftrightarrow 8{a^4} - 81{a^2}{x^2} + 81{a^4} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{{\left( {\frac{x}{a}} \right)}^2} = 9}\\{{{\left( {\frac{x}{a}} \right)}^2} = \frac{9}{8}}\end{array}} \right.\).
\({\left( {\frac{x}{a}} \right)^2} = \frac{9}{8}\) không thỏa mãn vì \(x < a\sqrt 2 \).
\({\left( {\frac{x}{a}} \right)^2} = 9 \Leftrightarrow x = 3a\). Suy ra \(SO = {(3a)^2} - {a^2} = 8{a^2}\).
Ta có : \(d\left( {AB;SD} \right) = d\left( {AB;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right) = 2d\left( {O;\left( {SCD} \right)} \right)\).
Gọi \(E\) là trung điểm của \(CD\), kẻ \(OH \bot SE\), khi đó \(d\left( {O;\left( {SCD} \right)} \right) = OH\).
\(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{E{O^2}}} = \frac{1}{{8{a^2}}} + \frac{2}{{{a^2}}} \Rightarrow OH = \frac{{2\sqrt 2 }}{{17}}\).
Suy ra \(d\left( {AB;CD} \right) = 2OH = \frac{{4\sqrt {34} }}{{17}}a\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là "2/3"
Phương pháp giải
Xác suất có điều kiện.
Lời giải
Gọi A là biến cố "người được chọn là nam"
Gọi \(B\) là biến cố "Người được chọn là người phải trực"
Khi đó ta có \(\overline A \) là biến cố "người được chọn là nữ", suy ra \[P\left( {\overline A } \right) = \frac{{30}}{{100}} = \frac{3}{{10}}\].
Là biến cố "người được chọn là nữ gần cơ quan", suy ra \(P\left( {B\overline A } \right) = \frac{{60 - 40}}{{100}} = \frac{2}{{10}}\).
Xác suất người được chọn là nữ và là người trực cơ quan là
\(P\left( {B\mid A} \right) = \frac{{P\left( {B\overline A } \right)}}{{P\left( {\overline A } \right)}} = \frac{{\frac{2}{{10}}}}{{\frac{3}{{10}}}} = \frac{2}{3}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là "10"
Phương pháp giải
Công thức tích phân.
Lời giải
Ta có \(v\left( 6 \right) = {v_0} \Leftrightarrow a = {v_0} + 15\) suy ra \(v\left( t \right) = \frac{{ - 5}}{2}t + {v_0} + 15\).
Gọi \(n\) là thời điểm vật dừng hẳn, khi đó ta có
\(v\left( n \right) = 0 \Leftrightarrow n = \frac{2}{5}\left( {{v_0} + 15} \right) \Leftrightarrow n = \frac{{2{v_0}}}{5} + 6\).
Khi đó ta có phương trình tổng quãng đường vật đi được là
\( \Leftrightarrow 80 = 6.{v_0} - \frac{5}{4}\left( {{n^2} - {6^2}} \right) + {v_0}\left( {n - 6} \right) + 15\left( {n - 6} \right)\)
\( \Leftrightarrow 80 = 6.{v_0} - \frac{5}{4}\left( {\frac{{4{{\left( {{v_0}} \right)}^2}}}{{25}} + \frac{{24{v_0}}}{{25}}} \right) + {v_0}\frac{{2{v_0}}}{5} + 15\frac{{2{v_0}}}{5}\)
\( \Leftrightarrow v_0^2 + 36{v_0} - 400 = 0 \Leftrightarrow {v_0} = 10\).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập