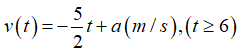Một ông chủ dãy trọ có 80 phòng trọ cho thuê. Ông nhận thấy rằng tất cả phòng trọ sẽ có người thuê nếu giá thuê một phòng trọ là 6 triệu đồng/tháng. Trong khi, khảo sát thị trường cho thấy trung bình cứ mỗi lần tăng giá trọ thêm 200 nghìn đồng/tháng thì sẽ có thêm 2 phòng trọ bị bỏ trống. Để ông chủ thu về được số tiền lớn nhất thì cần cho thuê bao nhiêu phòng trọ? (nhập đáp án vào ô trống)
Đáp án: ___
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là "60"
Phương pháp giải
Xây dựng hàm cần đánh giá và đưa về một ẩn.
Lời giải
Gọi \(x\) là số lần tăng giá trọ, khi đó ta có phương trình tổng số tiền mỗi tháng của ông chủ dựa theo \(x\) là:
\(y = \left( {6 + x.0,2} \right)\left( {80 - 2.x} \right)\) (1)
Khi đó ta cần tìm giá trị lớn nhất của hàm số trên:
\(\left( 1 \right) \Leftrightarrow y = - 0,4{x^2} + 4x + 480 \Rightarrow y' = - 0,4x + 4 = 0 \Leftrightarrow x = 10\).
Dễ thấy hàm số có giá trị lớn nhất tại \(x = 10\).
Vậy sẽ có 10 lần tăng tiền nhà tương ứng với 20 phòng sẽ bị trống.
Vây ông chủ sẽ thu được số tiền lớn nhất nếu cho thuê 60 phòng.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Cách để giải phóng bản thân khỏi những cảm xúc tiêu cực.
B. Tác hại của việc giữ lại những cảm xúc tiêu cực và giận dữ trong lòng.
C. Tầm quan trọng của cuộc sống đầy tình yêu thương.
D. Sự cần thiết của việc tha thứ và ảnh hưởng tích cực của nó đối với cuộc sống cá nhân.
Lời giải
Đáp án đúng là D
Phương pháp giải
Căn cứ vào nội dung toàn bài đọc.
Dạng bài đọc hiểu văn bản văn học - Câu hỏi kết hợp
Lời giải
- Nội dung đầy đủ nhất của đoạn trích: sự cần thiết của việc tha thứ và ảnh hưởng tích cực của nó đối với cuộc sống cá nhân. Đáp án này nêu đầy đủ và nhấn mạnh tầm quan trọng của việc tha thứ và tác động tích cực của nó đến tâm hồn và cuộc sống của con người.
- Phân tích, loại trừ: các đáp án A, B, và C không đúng vì chúng chỉ đề cập đến những khía cạnh riêng lẻ của nội dung đoạn trích mà không bao quát hết ý chính.
Câu 2
A. Miêu tả, biểu cảm
B. Biểu cảm, miêu tả, tự sự
C. Tự sự, miêu tả
D. Nghị luận, miêu tả, tự sự
Lời giải
Đáp án đúng là B
Phương pháp giải
Căn cứ vào các phương thức biểu đạt đã học
Dạng bài đọc hiểu văn bản văn học - Câu hỏi kết hợp
Lời giải
- Phương thức biểu đạt xuất hiện trong đoạn trích trên là tự sự, miêu tả, biểu cảm:
+ Tự sự: kể lại diễn biến trạng thái của Sài sau khi tỉnh dậy và đi tìm bạn.
+ Miêu tả: miêu tả trạng thái tâm lý của nhân vật Sài.
+ Biểu cảm: đoạn trích đan xen một số biểu cảm của nhân vật Sài khi chưa tìm thấy bạn và lúc đã thấy bạn.
Câu 3
A. Làm rõ lợi ích của việc tiêu thụ nước ép so với thực phẩm đặc.
B. Bác bỏ suy nghĩ đề cao giá trị của thực phẩm đặc mà xem nhẹ nước ép.
C. Đưa ra lời khuyên dinh dưỡng và hướng tới sự cân bằng trong cuộc sống.
D. Trình bày các cách thức để đưa thức ăn vào cơ thể có hiệu quả nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Sự xót đau, quặn thắt của nhân vật trữ tình.
B. Sự băn khoăn, trăn trở của nhân vật trữ tình.
C. Sự dõi theo, day dứt của nhân vật trữ tình.
D. Sự chia cách của không gian giữa mẹ và con.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Sau bước 2, có khí mùi thơm bay lên là mùi của etyl axetat.
B. Mục đích của việc làm lạnh là tạo môi trường nhiệt độ thấp giúp cho hơi etyl axetat ngưng tụ.
C. Để tăng hiệu suất phản ứng, ở bước 2 nên đun sôi hỗn hợp thay vì chỉ đun hỗn hợp ở nhiệt độ 65oC – 70oC.
D. Sau bước 2, trong ống nghiệm vẫn còn C2H5OH và CH3COOH.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Sự giao lưu của Hà Nội và các tỉnh thành khác khi kết thúc chiến tranh.
B. Cuộc sống khốn đốn của thủ đô trong thời kỳ chiến tranh chống giặc Mỹ.
C. Không khí của thủ đô Hà Nội trong những ngày thống nhất đất nước năm 1975.
D. Sự phát triển của Hà Nội từ khi chiến tranh kết thúc trên toàn quốc.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 18.
B. 7,2.
C. 6.
D. 7,5.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập