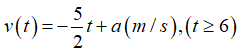Bảng dưới cho biết thời gian di chuyển tính bằng phút của các tuyến xe buýt giữa các bến xe \(A,B,C,D,E\). Số nằm tại ô giao của hàng cột là số phút xe buýt đi từ bến này đến bến kia, dấu \( \times \) biểu thị giữa hai bến này không có tuyến xe buýt. Bạn Lan đi từ bến xe \(A\) đến bến xe \(D\) bằng cung đường nhanh nhất thì mất bao nhiêu phút (không kể thời gian chờ xe buýt)

	A	B	C	D	E
A		30	20	\( \times \)	30
B			45	60	30
C				45	30
D					30
E

Đáp án đúng là "2/3"

Phương pháp giải

Xác suất có điều kiện.

Lời giải

Gọi A là biến cố "người được chọn là nam"

Gọi \(B\) là biến cố "Người được chọn là người phải trực"

Khi đó ta có \(\overline A \) là biến cố "người được chọn là nữ", suy ra \[P\left( {\overline A } \right) = \frac{{30}}{{100}} = \frac{3}{{10}}\].

Là biến cố "người được chọn là nữ gần cơ quan", suy ra \(P\left( {B\overline A } \right) = \frac{{60 - 40}}{{100}} = \frac{2}{{10}}\).

Xác suất người được chọn là nữ và là người trực cơ quan là

\(P\left( {B\mid A} \right) = \frac{{P\left( {B\overline A } \right)}}{{P\left( {\overline A } \right)}} = \frac{{\frac{2}{{10}}}}{{\frac{3}{{10}}}} = \frac{2}{3}\).

Đáp án đúng là "10"

Phương pháp giải

Công thức tích phân.

Lời giải

Ta có \(v\left( 6 \right) = {v_0} \Leftrightarrow a = {v_0} + 15\) suy ra \(v\left( t \right) = \frac{{ - 5}}{2}t + {v_0} + 15\).

Gọi \(n\) là thời điểm vật dừng hẳn, khi đó ta có

\(v\left( n \right) = 0 \Leftrightarrow n = \frac{2}{5}\left( {{v_0} + 15} \right) \Leftrightarrow n = \frac{{2{v_0}}}{5} + 6\).

Khi đó ta có phương trình tổng quãng đường vật đi được là

\( \Leftrightarrow 80 = 6.{v_0} - \frac{5}{4}\left( {{n^2} - {6^2}} \right) + {v_0}\left( {n - 6} \right) + 15\left( {n - 6} \right)\)

\( \Leftrightarrow 80 = 6.{v_0} - \frac{5}{4}\left( {\frac{{4{{\left( {{v_0}} \right)}^2}}}{{25}} + \frac{{24{v_0}}}{{25}}} \right) + {v_0}\frac{{2{v_0}}}{5} + 15\frac{{2{v_0}}}{5}\)

\( \Leftrightarrow v_0^2 + 36{v_0} - 400 = 0 \Leftrightarrow {v_0} = 10\).