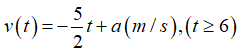Vòng đời của ếch bắt đầu từ khi trứng nở thành nòng nọc. Nòng nọc sống dưới nước, hô hấp bằng mang và có đuôi. Sau đó nòng nọc mất đuôi và mọc chân trở thành ếch. Ếch trưởng thành là loài lưỡng cư, hô hấp qua da và phổi. Hãy cho biết ếch nhái phát triển theo hình thức nào?
Vòng đời của ếch bắt đầu từ khi trứng nở thành nòng nọc. Nòng nọc sống dưới nước, hô hấp bằng mang và có đuôi. Sau đó nòng nọc mất đuôi và mọc chân trở thành ếch. Ếch trưởng thành là loài lưỡng cư, hô hấp qua da và phổi. Hãy cho biết ếch nhái phát triển theo hình thức nào?
A. Phát triển qua biến thái hoàn toàn.
B. Phát triển qua biến thái không hoàn toàn.
C. Phát triển không qua biến thái.
D. Phát triển qua biến thái.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là A
Phương pháp giải
Đọc lý thuyết các hình thức phát triển ở động vật.
Lời giải
Động vật phát triển qua biến thái hoặc không qua biến thái.
- Phát triển qua biến thái:
+ Biến thái hoàn toàn: Con non mới nở có hình dạng, cấu tạo và sinh lí rất khác so với con trưởng thành. Cơ thể con non phải trải qua nhiều biến đổi mới trở thành con trưởng thành (Ví dụ: muỗi, ếch,...)
+ Biến thái không hoàn toàn: Con non mới nở đã có hình dạng, cấu tạo và sinh lí gần giống con trưởng thành nhưng cần trải qua nhiều lần lột xác mới biến đổi thành con trưởng thành. (Ví dụ: châu chấu, gián,...)
- Phát triển không qua biến thái: Con non mới nở hoặc mới sinh có hình thái, cấu tạo và sinh lí tương tự con trưởng thành. Ví dụ: gà, mèo,...
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Làm rõ lợi ích của việc tiêu thụ nước ép so với thực phẩm đặc.
B. Bác bỏ suy nghĩ đề cao giá trị của thực phẩm đặc mà xem nhẹ nước ép.
C. Đưa ra lời khuyên dinh dưỡng và hướng tới sự cân bằng trong cuộc sống.
D. Trình bày các cách thức để đưa thức ăn vào cơ thể có hiệu quả nhất.
Lời giải
Đáp án đúng là A
Phương pháp giải
Căn cứ vào nội dung toàn bài đọc.
Dạng bài đọc hiểu văn bản văn học - Câu hỏi kết hợp
Lời giải
- Mục đích chính của đoạn trích là giải thích sự khác biệt giữa nước ép và thực phẩm đặc trong quá trình tiêu hóa, đồng thời nhấn mạnh những lợi ích mà nước ép mang lại, như khả năng tiêu hóa nhanh và hiệu quả hơn so với thực phẩm đặc.
- Phân tích, loại trừ:
+ Đáp án B sai vì bài đọc không nhắc tới nội dung này.
+ Đáp án C sai vì tác giả không đưa ra lời khuyên mà bài đọc chỉ đơn thuần trình bày những lợi ích của nước ép so với thực phẩm ở dạng thô.
+ Đáp án D sai vì đoạn trích cũng không hướng dẫn người đọc cách thức đưa thức ăn vào cơ thể.
Câu 2
A. Miêu tả, biểu cảm
B. Biểu cảm, miêu tả, tự sự
C. Tự sự, miêu tả
D. Nghị luận, miêu tả, tự sự
Lời giải
Đáp án đúng là B
Phương pháp giải
Căn cứ vào các phương thức biểu đạt đã học
Dạng bài đọc hiểu văn bản văn học - Câu hỏi kết hợp
Lời giải
- Phương thức biểu đạt xuất hiện trong đoạn trích trên là tự sự, miêu tả, biểu cảm:
+ Tự sự: kể lại diễn biến trạng thái của Sài sau khi tỉnh dậy và đi tìm bạn.
+ Miêu tả: miêu tả trạng thái tâm lý của nhân vật Sài.
+ Biểu cảm: đoạn trích đan xen một số biểu cảm của nhân vật Sài khi chưa tìm thấy bạn và lúc đã thấy bạn.
Câu 3
A. Cách để giải phóng bản thân khỏi những cảm xúc tiêu cực.
B. Tác hại của việc giữ lại những cảm xúc tiêu cực và giận dữ trong lòng.
C. Tầm quan trọng của cuộc sống đầy tình yêu thương.
D. Sự cần thiết của việc tha thứ và ảnh hưởng tích cực của nó đối với cuộc sống cá nhân.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Sự xót đau, quặn thắt của nhân vật trữ tình.
B. Sự băn khoăn, trăn trở của nhân vật trữ tình.
C. Sự dõi theo, day dứt của nhân vật trữ tình.
D. Sự chia cách của không gian giữa mẹ và con.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Sau bước 2, có khí mùi thơm bay lên là mùi của etyl axetat.
B. Mục đích của việc làm lạnh là tạo môi trường nhiệt độ thấp giúp cho hơi etyl axetat ngưng tụ.
C. Để tăng hiệu suất phản ứng, ở bước 2 nên đun sôi hỗn hợp thay vì chỉ đun hỗn hợp ở nhiệt độ 65oC – 70oC.
D. Sau bước 2, trong ống nghiệm vẫn còn C2H5OH và CH3COOH.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 18.
B. 7,2.
C. 6.
D. 7,5.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Sự giao lưu của Hà Nội và các tỉnh thành khác khi kết thúc chiến tranh.
B. Cuộc sống khốn đốn của thủ đô trong thời kỳ chiến tranh chống giặc Mỹ.
C. Không khí của thủ đô Hà Nội trong những ngày thống nhất đất nước năm 1975.
D. Sự phát triển của Hà Nội từ khi chiến tranh kết thúc trên toàn quốc.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập