Cho bảng số liệu về GDP và số dân của Hoa Kỳ giai đoạn 2000 – 2020:

Dựa vào bảng số liệu, nhận xét nào sau đây không đúng về GDP bình quân đầu người của Hoa Kỳ giai đoạn 2000 - 2020?
Cho bảng số liệu về GDP và số dân của Hoa Kỳ giai đoạn 2000 – 2020:

Dựa vào bảng số liệu, nhận xét nào sau đây không đúng về GDP bình quân đầu người của Hoa Kỳ giai đoạn 2000 - 2020?
Quảng cáo
Trả lời:
Đáp án đúng là A
Phương pháp giải
Nhận xét bảng số liệu và dựa vào công thức tính GDP bình quân đầu người.
Lời giải
- Công thức:
GDP bình quân đầu người = GDP/số dân.
- Ví dụ, tính GDP bình quân đầu người năm 2000:
+ Đổi 10 250,9 tỉ USD = 10 250 900 triệu USD
=> GDP bình quân đầu người năm 2010 là: 10 250 900/282,2 = 36 324,9 USD/người.
- Tính tương tự, GDP bình quân đầu người năm 2005, 2010 và 2020 lần lượt là: 44 125,9 USD/người; 48 655,0 USD/người; 63 027,8 USD/người.
=> GDP bình quân đầu người tăng không liên tục là nhận xét không đúng vì GDP bình quân đầu người của Hoa Kỳ tăng liên tục.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
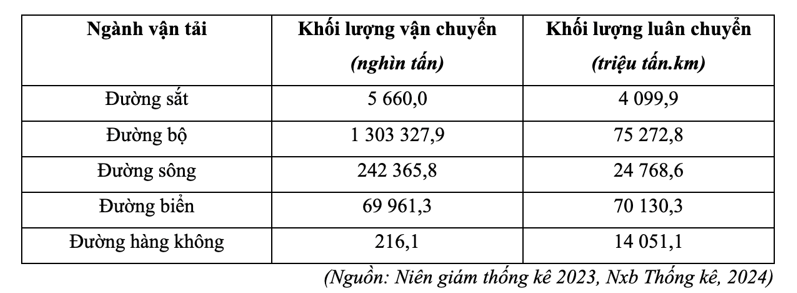
C. Đường sắt có cự li vận chuyển trung bình nhỏ hơn đường bộ.
Lời giải
Đáp án đúng là A
Phương pháp giải
Nhận xét bảng số liệu.
Lời giải
- Công thức:
Cự li vận chuyển trung bình = Khối lượng luân chuyển/Khối lượng vận chuyển.
- Dựa vào công thức tính trên, ta có bảng số liệu sau:
Cự li vận chuyển hàng hóa trung bình phân theo ngành vận tải của nước ta năm 2021
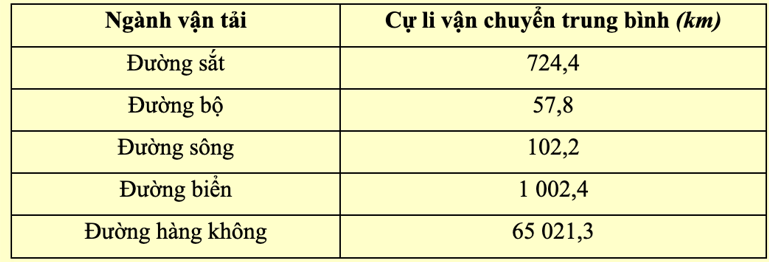
=> Đường hàng không có cự li vận chuyển trung bình dài nhất là nhận xét đúng.
Lời giải
Đáp án đúng là "2640"
Phương pháp giải
Tính giá trị nhỏ nhất
Lời giải
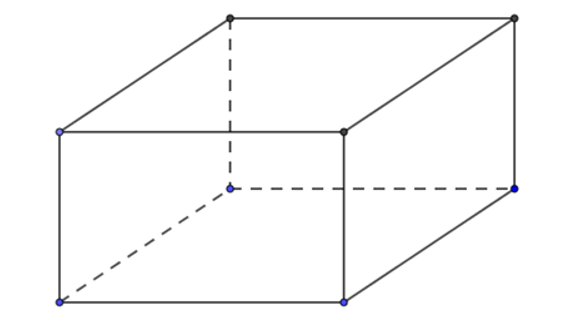
Gọi \(x,y\) lần lượt là chiều rộng và chiều dài của đáy hình hộp.
Điều kiện: \(x > 0;y > 0\left( m \right)\).
Ta có thể tích của khối hộp: \(V = 1xy = 400 \Rightarrow xy = 400 \Rightarrow y = \frac{{400}}{x}\left( {{m^3}} \right)\).
Diện tích mặt đáy: \({S_d} = xy = x.\frac{{400}}{x} = 400\left( {{{\rm{m}}^2}} \right)\).
Giá tiền để làm mặt đáy là: \(400.4000000 = {16.10^8}\) (đồng).
Diện tích xung quanh của bể cá: \({S_{xq}} = 2.x.1 + 2.y.1 = 2.\left( {x + y} \right) = 2.\left( {x + \frac{{400}}{x}} \right)\).
Giá tiền để làm mặt bên là: \(2.\left( {x + \frac{{400}}{x}} \right).3000000 = {6.10^6}.\left( {x + \frac{{400}}{x}} \right)\).
Tổng chi phí để xây dựng bể cá là:
\(T\left( x \right) = {6.10^6}.\left( {x + \frac{{400}}{x}} \right) + {24.10^8} \ge {6.10^6}.2\sqrt {x.\frac{{400}}{x}} + {24.10^8} \approx 2640{\rm{\;}}\) (triệu đồng).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.