(1,0 điểm)

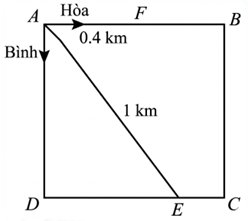
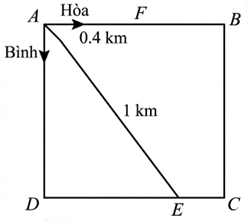
Từ vị trí \(A\) của một công viên có dạng hình vuông \(ABCD\) cạnh \(a\,\,{\rm{(km}})\), hai bạn Hòa và Bình bắt đầu chạy bộ cùng lúc với vặn tốc không đổi dọc theo các cạnh cùa hình vuông và theo hai hướng khác nhau. Biết rằng, hai bạn gặp nhau lần thứ nhất tại vị trí \(E\) cách \(A\) một khoảng bằng 1 km và gặp lại nhau là̀n thứ hai tại vị trí \(F\) cách \(A\) một khoảng bằng \(0,4{\rm{\;km}}\) như hình vẽ. Gọi \(x,\,\,y\,\,\left( {{\rm{km}}\,{\rm{/}}\,{\rm{h}}} \right)\) lần lượt là vận tốc cùa Hòa và Bình.

a) Chứng minh ràng \(\frac{x}{y} = \frac{{AB + BC + CE}}{{AD + DE}}\).

b) Tìm giá trị của \(a\).

Từ một điểm \(A\) nằm ngoài đường tròn \(\left( {O;R} \right)\) với \(OA = 2R\), kẻ hai tiếp tuyến \(AB,\,\,AC\) đến đường tròn (\(B,C\) là các tiếp điểm). Vẽ đường kính \(BD\) cùa đường tròn \(\left( O \right)\). Gọi \(E\) là giao điểm thứ hai của đường thẳng \(AD\) với \(\left( O \right)\). Đường thẳng \(BC\) và \(AO\) cắt nhau tại \(H.\)

a)

Chứng minh rằng tam giác \(BED\) vuông và \(ABHE\) là tứ giác nội tiếp.

Xét \(\Delta BED\) có \(\widehat {BED} = 90^\circ \) (tính chất góc nội tiếp chắn nửa đường tròn)

Suy ra \(\widehat {BEA} = 180^\circ - \widehat {BED} = 90^\circ .\)
Ta có: \(\Delta AOB = \Delta AOC\) (cạnh huyền – cạnh góc vuông).
Suy ra \(AB = AC\), suy ra \(\Delta ABC\) cân tại \(A\) và \(AO\) là phân giác của góc \(\widehat {BAC}.\)
Suy ra \(AO\) là đường cao \(\Delta ABC\) nên \(AO \bot BC\) suy ra \(\widehat {AHB} = 90^\circ .\)
Ta có \(\widehat {AHB} = 90^\circ \) nên \(A,\,\,H,\,\,B\) thuộc đường tròn đường kính \(AB\).
Vì \(\widehat {AEB} = 90^\circ \) nên \(A,\,\,E,\,\,B\) thuộc đường tròn đường kính \(AB\).
Suy ra \(A,H,B,E\) thuộc đường tròn, hay tứ giác \(AEBH\) nội tiếp.

Vậy tam giác \(BED\) vuông và \(ABHE\) là tứ giác nội tiếp.

b)

Chứng minh rà̀ng \(O{D^2} = OH \cdot OA\) và \(\widehat {HDO} = \widehat {HBE}\).

Xét \(\Delta OBA\) và \(\Delta OHB\) có: \(\widehat {AOB}\) chung, \(\widehat {OBA} = \widehat {OHB}\).

Do đó  suy ra \(\frac{{OB}}{{OH}} = \frac{{OA}}{{OB}}\) nên \(O{B^2} = OA \cdot OH\).
Vì \(OB = OD = R\) nên ta có: \(OA \cdot OH = O{D^2}\) (đpcm).
Xét \(\Delta ODH\) và \(\Delta OAD\) có \(\frac{{OD}}{{OA}} = \frac{{OH}}{{OD}}\) (cmt), \(\widehat {AOD}\) chung.
Suy ra  (c.g.c)
Suy ra \(\widehat {ODH} = \widehat {OAD}\) (hai góc tương ứng).

Mà \(\widehat {HAE} = \widehat {HBE}\) (hai góc nội tiếp cùng chắn  nên \(\widehat {ODH} = \widehat {OBE}\).

Vậy \(O{D^2} = OH \cdot OA\) và \(\widehat {ODH} = \widehat {OBE}\).

c)

Tính theo \(R\) chu vi và diện tích tam giác DHE.

Ta có \(\Delta OBA\) vuông có \(AB = \sqrt {O{A^2} - O{B^2}} = R\sqrt 3 \)
\(\Delta ABD\) vuông có \(A{D^2} = A{B^2} + B{D^2}\), suy ra \(AD = R\sqrt 7 \).
Mặt khác,  (g.g) nên \(\frac{{DE}}{{DB}} = \frac{{DB}}{{DA}}\), suy ra \(DE \cdot DA = D{B^2}\).

Từ đó \(DE = \frac{{4{R^2}}}{{R\sqrt 7 }} = \frac{{4R\sqrt 7 }}{7}\).
Vì \(OH \bot BC,\,\,DC \bot BC\) nên \(OH\,{\rm{//}}\,DC\).

Mà \(O\) là trung điểm \(BD\) nên được \(OH\) là đường trung bình của tan giác \(BDC\).

Suy ra \(OH = \frac{1}{2}CD\) hay \(CD = 2OH\).

Lại có \(OH \cdot OA = O{B^2}\) hay \(OH = \frac{R}{2}\) suy ra \(CD = R\) nên \(\Delta DCH\) vuông.

Từ đó \(DH = \sqrt {D{C^2} + H{C^2}} = \frac{{R\sqrt 7 }}{2}\); \(HC = \sqrt {O{C^2} - O{H^2}} = \frac{{R\sqrt 3 }}{2}.\)
Ta có \(\widehat {AHE} = \widehat {ABE},\,\,\widehat {ABE} = \widehat {ADB}\) (cùng phụ với góc \(\widehat {EAH}\,)\) nên \(\widehat {AHE} = \widehat {ADB}\)

Do đó

Suy ra \(\frac{{EH}}{{OD}} = \frac{{AD}}{{AD}} = \frac{{AO - OH}}{{AO}} = \frac{{3R\sqrt 7 }}{{14}}\) hay \(EH = \frac{{3R\sqrt 7 }}{{14}}.\)

Khi đó chu vi tam giác \(EHD\) là: \(EH + DH + DE = \frac{{3R\sqrt 7 }}{{14}} + \frac{{R\sqrt 7 }}{2} + \frac{{4R\sqrt 7 }}{7} = \frac{{9R\sqrt 7 }}{7}\).
Tính diện tích: \(\widehat {BAO} = \widehat {BEH} = 30^\circ \) nên \(\widehat {HED} = 90^\circ - 30^\circ = 60^\circ .\)
Gọi \(K\) là hình chiếu của \(H\) xuống \(DE\), ta có:

\[{\rm{sin}}\,60^\circ = \frac{{HK}}{{HE}}\] nên \(HK = \frac{{3R\sqrt 7 }}{{14}} \cdot \frac{{\sqrt 3 }}{2} = \frac{{3R\sqrt {21} }}{{28}}\).
Khi đó, diện tích tam giác \(DHE\) là \(S = \frac{1}{2} \cdot HK \cdot DE = \frac{1}{2} \cdot \frac{{3R\sqrt {21} }}{{28}} \cdot \frac{{4R\sqrt 7 }}{7} = \frac{{3{R^2}\sqrt 3 }}{{14}}\).
Vậy diện tích tam giác \(DHE\) là \(\frac{{3{R^2}\sqrt 3 }}{{14}}\).

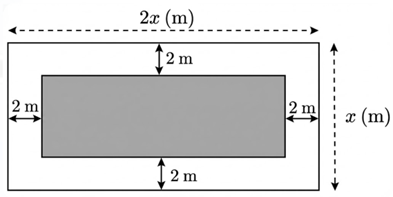
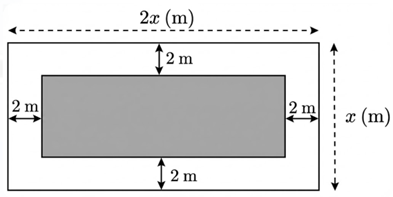
Một khu vườn hình chữ nhật có chiều dài là \(2x\,\,\left( {\rm{m}} \right)\) và chiều rộng là \(x\left( m \right),\)\(x > 4.\) Bác Ba làm một lối đi quanh khu vırờn rộng 2 mẹt như hình vẽ. Phần đất còn lại (phần in đậm) dùng để trồng hoa.

a)

Viết biểu thức theo \(x\) biểu diễn diện tích phần đất dùng để trồng hoa và thu gọn biểu thức đó.

Chiều rộng của phần đất dùng đề trồng hoa là: \(x - 2.2 = x - 4\left( {{\rm{\;m}}} \right)\)

Chiều dài của phần đất dùng để trồng hoa là: \(2x - 2.2 = 2x - 4\left( {{\rm{\;m}}} \right)\)

Diện tích phần đất dùng để trồng hoa là \(S = \left( {x - 4} \right)\left( {2x - 4} \right)\left( {{m^2}} \right)\)

Thu gọn biểu thức: \(S = \left( {x - 4} \right)\left( {2x - 4} \right) = 2{x^2} - 4x - 8x + 16\)\[ = 2{x^2} - 12x + 16\].

Vậy biĉ̉u thức biểu diễn diện tích phần đất dùng để trồng hoa là \[S = 2{x^2} - 12x + 16\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right).\]

b)

Giả sử diện tích phần đất trồng hoa là \(4800{\rm{\;}}{{\rm{m}}^2}\). Tính chiều dài và chiều rộng của khu vườn.

Diện tích phần đất trồng hoa là \(4800{\rm{\;}}{{\rm{m}}^2}\) nên ta có \(2{x^2} - 12x + 16 = 4800\).

Giải phương trình: \(2{x^2} - 12x + 16 = 4800\)

\({x^2} - 6x + 8 = 2400\)

\({x^2} - 6x - 2392 = 0\)

Ta có \({\rm{\Delta }} = {( - 6)^2} - 4.1 \cdot \left( { - 2392} \right) = 9604 > 0\) nên phương trình có 2 nghiệm phân biệt: \({x_1} = \frac{{6 + \sqrt {9604} }}{2} = 5\) (TMĐK); \({x_2} = \frac{{6 - \sqrt {9604} }}{2} = - 46\) (loại)

Vậy chiều rộng của khu vườn là 52 m, chiều dài của khu vườn là \(2 \cdot 52 = 104\,\,({\rm{m}}).\)