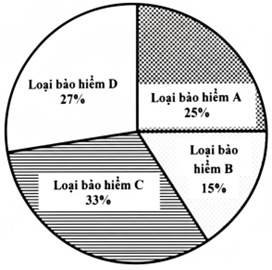
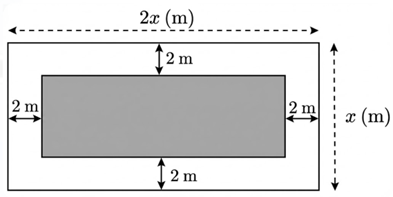
(1,5 điểm) Biểu đồ tròn cho biết tỉ lệ về số lượng các loại bảo hiểm đã bán được trong tháng 4/2025 của một công ty. Biết rằng trong tháng này, công ty đã bán được 300 gói bảo hiểm các loại cho 300 khách hàng khác nhau.

a) Tính số lượng cụ thể của mỗi loại bảo hiểm mà công ty đã bán được trong tháng 4/2025?

b) Bộ phận chăm sóc khách hàng chọn ngẫu nhiên một khách hàng đã mua bảo hiểm cùa công ty trong tháng 4/2025 đề khảo sát. Tính xác suất của biến cố: “Khách hàng được chọn không mua loại bào hiểm B”.

Từ một điểm \(A\) nằm ngoài đường tròn \(\left( {O;R} \right)\) với \(OA = 2R\), kẻ hai tiếp tuyến \(AB,\,\,AC\) đến đường tròn (\(B,C\) là các tiếp điểm). Vẽ đường kính \(BD\) cùa đường tròn \(\left( O \right)\). Gọi \(E\) là giao điểm thứ hai của đường thẳng \(AD\) với \(\left( O \right)\). Đường thẳng \(BC\) và \(AO\) cắt nhau tại \(H.\)

a)

Chứng minh rằng tam giác \(BED\) vuông và \(ABHE\) là tứ giác nội tiếp.

Xét \(\Delta BED\) có \(\widehat {BED} = 90^\circ \) (tính chất góc nội tiếp chắn nửa đường tròn)

Suy ra \(\widehat {BEA} = 180^\circ - \widehat {BED} = 90^\circ .\)
Ta có: \(\Delta AOB = \Delta AOC\) (cạnh huyền – cạnh góc vuông).
Suy ra \(AB = AC\), suy ra \(\Delta ABC\) cân tại \(A\) và \(AO\) là phân giác của góc \(\widehat {BAC}.\)
Suy ra \(AO\) là đường cao \(\Delta ABC\) nên \(AO \bot BC\) suy ra \(\widehat {AHB} = 90^\circ .\)
Ta có \(\widehat {AHB} = 90^\circ \) nên \(A,\,\,H,\,\,B\) thuộc đường tròn đường kính \(AB\).
Vì \(\widehat {AEB} = 90^\circ \) nên \(A,\,\,E,\,\,B\) thuộc đường tròn đường kính \(AB\).
Suy ra \(A,H,B,E\) thuộc đường tròn, hay tứ giác \(AEBH\) nội tiếp.

Vậy tam giác \(BED\) vuông và \(ABHE\) là tứ giác nội tiếp.

b)

Chứng minh rà̀ng \(O{D^2} = OH \cdot OA\) và \(\widehat {HDO} = \widehat {HBE}\).

Xét \(\Delta OBA\) và \(\Delta OHB\) có: \(\widehat {AOB}\) chung, \(\widehat {OBA} = \widehat {OHB}\).

Do đó  suy ra \(\frac{{OB}}{{OH}} = \frac{{OA}}{{OB}}\) nên \(O{B^2} = OA \cdot OH\).
Vì \(OB = OD = R\) nên ta có: \(OA \cdot OH = O{D^2}\) (đpcm).
Xét \(\Delta ODH\) và \(\Delta OAD\) có \(\frac{{OD}}{{OA}} = \frac{{OH}}{{OD}}\) (cmt), \(\widehat {AOD}\) chung.
Suy ra  (c.g.c)
Suy ra \(\widehat {ODH} = \widehat {OAD}\) (hai góc tương ứng).

Mà \(\widehat {HAE} = \widehat {HBE}\) (hai góc nội tiếp cùng chắn  nên \(\widehat {ODH} = \widehat {OBE}\).

Vậy \(O{D^2} = OH \cdot OA\) và \(\widehat {ODH} = \widehat {OBE}\).

c)

Tính theo \(R\) chu vi và diện tích tam giác DHE.

Ta có \(\Delta OBA\) vuông có \(AB = \sqrt {O{A^2} - O{B^2}} = R\sqrt 3 \)
\(\Delta ABD\) vuông có \(A{D^2} = A{B^2} + B{D^2}\), suy ra \(AD = R\sqrt 7 \).
Mặt khác,  (g.g) nên \(\frac{{DE}}{{DB}} = \frac{{DB}}{{DA}}\), suy ra \(DE \cdot DA = D{B^2}\).

Từ đó \(DE = \frac{{4{R^2}}}{{R\sqrt 7 }} = \frac{{4R\sqrt 7 }}{7}\).
Vì \(OH \bot BC,\,\,DC \bot BC\) nên \(OH\,{\rm{//}}\,DC\).

Mà \(O\) là trung điểm \(BD\) nên được \(OH\) là đường trung bình của tan giác \(BDC\).

Suy ra \(OH = \frac{1}{2}CD\) hay \(CD = 2OH\).

Lại có \(OH \cdot OA = O{B^2}\) hay \(OH = \frac{R}{2}\) suy ra \(CD = R\) nên \(\Delta DCH\) vuông.

Từ đó \(DH = \sqrt {D{C^2} + H{C^2}} = \frac{{R\sqrt 7 }}{2}\); \(HC = \sqrt {O{C^2} - O{H^2}} = \frac{{R\sqrt 3 }}{2}.\)
Ta có \(\widehat {AHE} = \widehat {ABE},\,\,\widehat {ABE} = \widehat {ADB}\) (cùng phụ với góc \(\widehat {EAH}\,)\) nên \(\widehat {AHE} = \widehat {ADB}\)

Do đó

Suy ra \(\frac{{EH}}{{OD}} = \frac{{AD}}{{AD}} = \frac{{AO - OH}}{{AO}} = \frac{{3R\sqrt 7 }}{{14}}\) hay \(EH = \frac{{3R\sqrt 7 }}{{14}}.\)

Khi đó chu vi tam giác \(EHD\) là: \(EH + DH + DE = \frac{{3R\sqrt 7 }}{{14}} + \frac{{R\sqrt 7 }}{2} + \frac{{4R\sqrt 7 }}{7} = \frac{{9R\sqrt 7 }}{7}\).
Tính diện tích: \(\widehat {BAO} = \widehat {BEH} = 30^\circ \) nên \(\widehat {HED} = 90^\circ - 30^\circ = 60^\circ .\)
Gọi \(K\) là hình chiếu của \(H\) xuống \(DE\), ta có:

\[{\rm{sin}}\,60^\circ = \frac{{HK}}{{HE}}\] nên \(HK = \frac{{3R\sqrt 7 }}{{14}} \cdot \frac{{\sqrt 3 }}{2} = \frac{{3R\sqrt {21} }}{{28}}\).
Khi đó, diện tích tam giác \(DHE\) là \(S = \frac{1}{2} \cdot HK \cdot DE = \frac{1}{2} \cdot \frac{{3R\sqrt {21} }}{{28}} \cdot \frac{{4R\sqrt 7 }}{7} = \frac{{3{R^2}\sqrt 3 }}{{14}}\).
Vậy diện tích tam giác \(DHE\) là \(\frac{{3{R^2}\sqrt 3 }}{{14}}\).

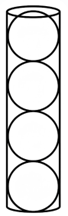
Một hộp đựng bóng tennis có dạng hình trụ chứa vừa khít 4 quả bóng tennis có dạng hình cầu như Hình 1. Biết diện tích bề mặt mỗi quả bóng tennis là \(132,67\,\,{\rm{c}}{{\rm{m}}^2}.\)

a)

Tính bán kính của mỗi quả bóng tennis.

Vì diện tích bề mặt mỗi quả bóng tennis là \(132,67{\rm{\;c}}{{\rm{m}}^2}\) nên \(4\pi {R^2} = 132,67\)

Suy ra \({R^2} = \frac{{132,67}}{{4\pi }} \approx 10,56\)

Do đó \(R \approx \sqrt {10,56} \approx 3,25\,\,{\rm{(cm}}).\)

Vậy bán kính mỗi quả bóng tennis khoảng \(3,25{\rm{\;cm}}\).

b)

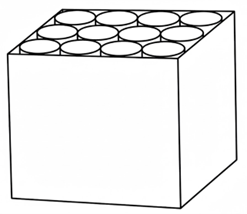
Nhà sản xuất thường sử dụng các thùng giấy hình hộp chữ nhật (có nắp) để chứa 12 hộp tennis sao cho các hộp tennis đượe xếp vùa khit trong thùng giấy như Hình 2. Hỏi cần tối thiếu bao nhiêu \({m^2}\) giấy đề thiết kế một thùng như trên (giả sử các mép nối không đáng kể). Các kết quả được làm tròn đến hàng phần trăm.

Mỗi hộp tennis chứa 4 quả tennis nên chiều cao của hộp tennis là:

                  \(4 \cdot 2R = 4 \cdot 2 \cdot 3,25 = 26\,\,{\rm{(cm}}).\)

Đường kinh đáy một hộp tennis là: \(2R = 2 \cdot 3,25 = 6,5\,\,{\rm{(cm}}).\).

Vi thùng giấy chứa được 12 hộp tennis \(\left( {3 \times 4} \right)\) nên chiều dài thùng giấy là: \(6,5 \cdot 4 = 26\,\,{\rm{(cm}}).\)

chiều rộng của thùng giấy là: \(6,5.3 = 19,5\,\,{\rm{(cm}}).\)

chiều cao của thùng giấy chinh là chiều cao của hộp tennis nên chiều cao cùa thùng giấy là 26 cm

Diện tích giấy để thiết kể một thùng (diện tích toàn phần của hình hộp chũ nhật) là: \[{S_{tp}} = 2\left( {ab + bc + ca} \right) \approx 2\left( {26.19,5 + 19,5.26 + 26.26} \right) = 3380\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\]

       \[ = 0,338\,\,\left( {{{\rm{m}}^2}} \right) \approx 0,34\,\,\left( {{{\rm{m}}^2}} \right).\]

Vậy cần tối thiểu \(0,34{\rm{\;}}{{\rm{m}}^2}\) giấy dể thiết kể một thùng như trên.