Người ta muốn sản xuất một bể nước theo dạng khối lăng trụ tứ giác đều, không có nắp trên, làm bằng kính và có thể tích là \(16\,{m^3}\). Biết giá của mỗi mét vuông kính là \(500\,000\) đồng. Số tiền tối thiểu phải trả để làm bể nước trên gần nhất với giá trị nào dưới đây?
A. \(15\,\,119\,\,053\) đồng.
B. \(15\,\,119\,\,052\) đồng.
C. \(15\,\,119\,\,051\) đồng.
D. \(15\,\,119\,\,050\) đồng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi cạnh đáy của bể nước có độ dài là \(x\left( m \right)\) và chiều cao của bể nước là \(h\left( m \right)\). Điều kiện \(x,h > 0\). Khi đó thể tích của bể nước là \(16\,{m^3}\) nên \({x^2}h = 16 \Leftrightarrow h = \frac{{16}}{{{x^2}}}\).
Diện tích cần để xây bể nước (bao gồm diện tích xung quanh và diện tích mặt đáy) là
\(S = 4xh + {x^2} = 4x.\frac{{16}}{{{x^2}}} + {x^2} = \frac{{64}}{x} + {x^2}\) (m2).
Để tìm số tiền tối thiểu, ta tìm giá trị nhỏ nhất của hàm số \(y = S\left( x \right)\) với \(x > 0\).
Ta có \(S'\left( x \right) = - \frac{{64}}{{{x^2}}} + 2x\). Cho \(S'\left( x \right) = 0 \Rightarrow 2{x^3} - 64 = 0 \Leftrightarrow x = \sqrt[3]{{32}}\).
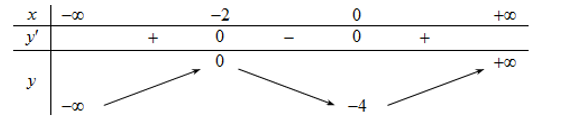
Lập bảng biến thiên, ta dễ thấy \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} S\left( x \right) = S\left( {\sqrt[3]{{32}}} \right)\).
Vậy số tiền tối thiểu phải trả là: \(500\,\,000 \cdot S\left( {\sqrt[3]{{32}}} \right) \approx 15\,\,119\,\,053\) (đồng). Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[\frac{1}{5}\].
B. \[\frac{{11}}{{23}}\].
C. \[\frac{{12}}{{23}}\].
D. \[\frac{{11}}{{19}}\].
Lời giải
Gọi A là biến cố “gọi được sinh viên nữ”.
Gọi B là biến cố “gọi được sinh viên đạt điểm giỏi môn xác suất thống kê”.
Ta đi tính \[P\left( {B|A} \right)\]. Ta có: \[P\left( A \right) = \frac{{55}}{{95}}\]; \[P\left( {A \cap B} \right) = \frac{{11}}{{95}}\].
Do đó: \[P\left( {B|A} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( A \right)}} = \frac{{11}}{{95}}:\frac{{55}}{{95}} = \frac{{11}}{{55}} = \frac{1}{5}\]. Chọn A.
Lời giải
Thay \(t = 2\) phút \( = \frac{1}{{30}}\) giờ, \({T_0} = 96\,,\,T = 90\,,\,S = 24\) ta có \(\frac{1}{{30}}k = \ln \frac{{90 - 24}}{{96 - 24}}\).
Do đó \(k = 30\ln \frac{{11}}{{12}}\).
Sau 10 phút \( = \frac{1}{6}\) giờ, ta có \(\frac{1}{6}k = \ln \frac{{T - 24}}{{96 - 24}}\) hay \(5\ln \frac{{11}}{{12}} = \ln \frac{{T - 24}}{{72}}\). Do đó \(\frac{{T - 24}}{{72}} = {\left( {\frac{{11}}{{12}}} \right)^5}\).
Suy ra \(T = 72 \cdot {\left( {\frac{{11}}{{12}}} \right)^5} + 24 \approx 70,6^\circ {\rm{C}}\). Vậy nhiệt độ của cốc trà sau 10 phút khoảng \(70,6^\circ {\rm{C}}\).
Đáp án cần nhập là: \(70,6\).
Câu 3
A. \(2\).
B. \(3\).
C. \(1\).
D. \(4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. The difficulties and challenges of repairing damaged historical sites and artifacts.
B. The benefits of using high-tech computers in the restoration process.
C. The role of artificial intelligence in predicting original architectures.
D. The process of scanning and connecting artifact pieces.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{{395}}{{24}}\,c{m^3}\).
B. \(\frac{{50}}{3}\,\,c{m^3}\).
C. \(\frac{{125}}{8}\,c{m^3}\).
D. \(\frac{{425}}{{24}}\,c{m^3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập