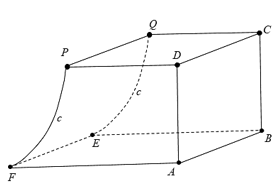
Một chi tiết máy được thiết kế như hình vẽ bên. Các tứ giác \(ABCD,CDPQ\) là các hình vuông cạnh \(2,5\,cm\). Tứ giác \(ABEF\) là hình chữ nhật có \(BE = 3,5\,cm\). Mặt bên \(PQEF\) được mài nhẵn theo đường parabol \(\left( P \right)\) có đỉnh parabol nằm trên cạnh \(EF.\) Thể tích của chi tiết máy bằng:
A. \(\frac{{395}}{{24}}\,c{m^3}\).
B. \(\frac{{50}}{3}\,\,c{m^3}\).
C. \(\frac{{125}}{8}\,c{m^3}\).
D. \(\frac{{425}}{{24}}\,c{m^3}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi hình chiếu của \[P,\,Q\] trên \[AF\] và \[BE\] là \[S\] và \[R\].
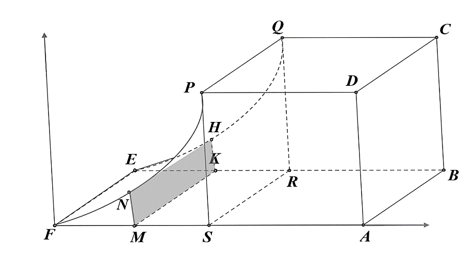
Chi tiết máy được chia thành hình lập phương \[ABCD.SRQP\] cạnh \[2,5\,cm\] có thể tích \({V_1} = \frac{{125}}{8}\,c{m^3}\) và phần còn lại có thể tích \[{V_2}\].
Khi đó thể tích chi tiết máy là: \[V = {V_1} + {V_2} = \frac{{125}}{8} + {V_2}\].
Đặt hệ trục \[Oxyz\] sao cho \[O\] trùng với \[F\], \[Ox\] trùng với \[FA\], \[Oy\] trùng với tia \[Fy\] song song với \[AD\]. Khi đó Parabol \[\left( P \right)\] có phương trình dạng \(y = a{x^2}\), đi qua điểm \[P\left( {1;\frac{5}{2}} \right)\], do đó \[a = \frac{5}{2} \Rightarrow y = \frac{5}{2}{x^2}\].
Cắt chi tiết máy bởi mặt phẳng vuông góc với \[Ox\] và đi qua điểm \[M\left( {x;0;0} \right),\,0 \le x \le 1\] ta được thiết diện là hình chữ nhật \[MNHK\] có cạnh là \(MN = \frac{5}{2}{x^2}\) và \(MK = \frac{5}{2}\), do đó diện tích thiết diện là \[S\left( x \right) = \frac{{25}}{4}{x^2}\]. Áp dụng công thức thể tích vật thể ta có: \[{V_2} = \int\limits_0^1 {\frac{{25}}{4}{x^2}dx} = \frac{{25}}{{12}}\].
Từ đó \[V = \frac{{125}}{8} + \frac{{25}}{{12}} = \frac{{425}}{{24}}\left( {c{m^3}} \right)\]. Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[\frac{1}{5}\].
B. \[\frac{{11}}{{23}}\].
C. \[\frac{{12}}{{23}}\].
D. \[\frac{{11}}{{19}}\].
Lời giải
Gọi A là biến cố “gọi được sinh viên nữ”.
Gọi B là biến cố “gọi được sinh viên đạt điểm giỏi môn xác suất thống kê”.
Ta đi tính \[P\left( {B|A} \right)\]. Ta có: \[P\left( A \right) = \frac{{55}}{{95}}\]; \[P\left( {A \cap B} \right) = \frac{{11}}{{95}}\].
Do đó: \[P\left( {B|A} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( A \right)}} = \frac{{11}}{{95}}:\frac{{55}}{{95}} = \frac{{11}}{{55}} = \frac{1}{5}\]. Chọn A.
Lời giải
Thay \(t = 2\) phút \( = \frac{1}{{30}}\) giờ, \({T_0} = 96\,,\,T = 90\,,\,S = 24\) ta có \(\frac{1}{{30}}k = \ln \frac{{90 - 24}}{{96 - 24}}\).
Do đó \(k = 30\ln \frac{{11}}{{12}}\).
Sau 10 phút \( = \frac{1}{6}\) giờ, ta có \(\frac{1}{6}k = \ln \frac{{T - 24}}{{96 - 24}}\) hay \(5\ln \frac{{11}}{{12}} = \ln \frac{{T - 24}}{{72}}\). Do đó \(\frac{{T - 24}}{{72}} = {\left( {\frac{{11}}{{12}}} \right)^5}\).
Suy ra \(T = 72 \cdot {\left( {\frac{{11}}{{12}}} \right)^5} + 24 \approx 70,6^\circ {\rm{C}}\). Vậy nhiệt độ của cốc trà sau 10 phút khoảng \(70,6^\circ {\rm{C}}\).
Đáp án cần nhập là: \(70,6\).
Câu 3
A. \(2\).
B. \(3\).
C. \(1\).
D. \(4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. The difficulties and challenges of repairing damaged historical sites and artifacts.
B. The benefits of using high-tech computers in the restoration process.
C. The role of artificial intelligence in predicting original architectures.
D. The process of scanning and connecting artifact pieces.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập