Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(A\) góc \(\widehat {ABC} = 30^\circ \); tam giác \(SBC\) là tam giác đều cạnh \(a\) và mặt phẳng \(\left( {SAB} \right)\) vuông góc mặt phẳng \(\left( {ABC} \right)\). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) là:
A. \(\frac{{a\sqrt 6 }}{5}\)
B. \(\frac{{a\sqrt 6 }}{3}\).
C. \(\frac{{a\sqrt 3 }}{3}\).
D. \(\frac{{a\sqrt 6 }}{6}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
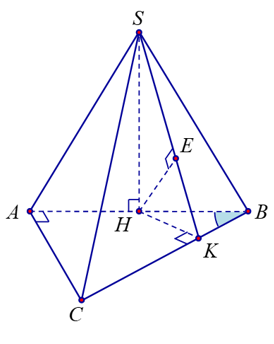
Ta có tam giác \(ABC\) vuông tại \(A\) có \(\widehat {ABC} = 30^\circ \) và \(BC = a\), suy ra \(AC = \frac{a}{2},\,AB = \frac{{a\sqrt 3 }}{2}\).
Lại có \[\,\,\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right)\\CA \bot AB\end{array} \right.\,\, \Rightarrow AC \bot \left( {SAB} \right)\], suy ra tam giác \(SAC\) vuông tại \(A\).
Suy ra \(SA = \sqrt {S{C^2} - A{C^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\).
Tam giác \(SAB\) có \(SA = \frac{{a\sqrt 3 }}{2},\,AB = \frac{{a\sqrt 3 }}{2},\,SB = a\).
Từ đó sử dụng công thức Heron ta tính được \({S_{SAB}} = \frac{{{a^2}\sqrt 2 }}{4}\).
\( \Rightarrow SH = \frac{{2{S_{SAB}}}}{{AB}} = \frac{{a\sqrt 6 }}{3} \Rightarrow BH = \frac{{a\sqrt 3 }}{3} = \frac{{2AB}}{3}\) (với \(H\) là hình chiếu vuông góc của \(S\) lên \(AB\)). Suy ra \(d\left( {H,\left( {SBC} \right)} \right) = \frac{2}{3}d\left( {A,\left( {SBC} \right)} \right).\) Từ \(H\) kẻ \(HK \bot BC\). Kẻ \(HE \bot SK \Rightarrow HE \bot \left( {SBC} \right)\).
Ta tính được \(HK = \frac{{a\sqrt 3 }}{6} \Rightarrow d\left( {H,\left( {SBC} \right)} \right) = HE = \frac{{a\sqrt 6 }}{9}.\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = \frac{3}{2}d\left( {H,\left( {SBC} \right)} \right) = \frac{3}{2} \cdot \frac{{a\sqrt 6 }}{9} = \frac{{a\sqrt 6 }}{6}\). Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Khi ô tô dừng lại, ta có \(v\left( t \right) = 0 \Leftrightarrow - 2t + 20 = 0 \Leftrightarrow t = 10\).
Vậy từ thời điểm đạp phanh đến khi dừng lại, ô tô di chuyển được thêm 10 giây và quãng đường đi được là: \(s = \int\limits_0^{10} {\left( { - 2t + 20} \right)\,} dt = \left. {\left( { - {t^2} + 20t} \right)} \right|_0^{10} = 100\) (m).
Trong 5 giây trước đó, ô tô vẫn đang đi với vận tốc \(20\;{\rm{m}}/{\rm{s}}\) nên quãng đường đi được trong 5 giây này là: \(5 \cdot 20 = 100\)(m).
Vậy quãng đường mà ô tô đi được trong 15 giây cuối cùng bằng: \(100 + 100 = 200\;\,\left( {\rm{m}} \right)\).
Đáp án cần nhập là: \(200\).
Lời giải
Gọi số mol và số mol \[{C_4}{H_{10}}\] lần lượt là a và 2a, ta có: \[{C_3}{H_8}\]
44a + 58.2a = 12.1000 Þ a = 75 mol
Nhiệt đốt cháy 12 kg gas là Q = 75.2220 + 150.2874 = 597600 (kJ)
Số ngày sử dụng hết bình gas = \(\frac{{597600}}{{10000.\frac{{100}}{{80}}}} = 47,808 \approx 48\) (ngày)
Chọn A.Câu 3
A. \[\frac{{x - 2}}{3} = \frac{{y - 1}}{1} = \frac{{z - 4}}{{ - 2}}\]
B. \[\frac{{x + 3}}{1} = \frac{{y + 2}}{{ - 2}} = \frac{{z + 2}}{2}\].
C. \[\frac{{x - 3}}{1} = \frac{y}{{ - 2}} = \frac{{z - 2}}{2}\].
D. \[\frac{{x + 3}}{{ - 1}} = \frac{{y - 2}}{2} = \frac{{z + 2}}{{ - 2}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Hành chính công vụ.
B. Nghị luận.
C. Thuyết minh.
D. Tự sự.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Nhiệt độ trung bình tháng VII cao nhất ở Huế vì chịu tác động mạnh mẽ của gió phơn khô nóng.
B. Ở TP. Hồ Chí Minh, nhiệt độ tháng VII thấp hơn các địa điểm khác vì đây là tháng có mưa lớn.
C. Nhiệt độ trung bình năm tăng dần từ Bắc vào Nam vì càng về phía Nam góc nhập xạ càng lớn, lượng nhiệt nhận được càng nhiều.
D. Tháng I, chênh lệch nhiệt độ giữa 2 miền Bắc Nam rõ rệt do miền Bắc chịu ảnh hưởng của gió mùa Đông Nam lạnh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. The historical spread and global impact of African swine fever (ASF).
B. The details of a specific ASF outbreak in Vietnam.
C. The methods used to control African swine fever (ASF) outbreaks.
D. The symptoms and effects of African swine fever (ASF) on pigs.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập