Tập hợp gồm hữu hạn điểm trên mặt phẳng sao cho với mọi điểm thuộc tồn tại đúng 4 điểm thuộc có khoảng cách đến bằng 1. Hỏi tập hợp có thể chứa ít nhất là bao nhiêu phần tử (nhập đáp án vào ô trống)?
Đáp án __
Quảng cáo
Trả lời:
Giải bởi Vietjack
Rõ ràng có ít nhất hai điểm \[P,Q\] thuộc \[M\] sao cho \[PQ \ne 1\] .
Ký hiệu: \[{M_P} = \left\{ {X \in M{\rm{ | }}PX = 1} \right\}\]. Từ giả thiết \[\left| {{M_P}} \right| = 4\], ta có: \[\left| {{M_P} \cap {M_Q}} \right| \le 2\].
Nếu tồn tại \[P,{\rm{ }}Q\] sao cho \[\left| {{M_P} \cap {M_Q}} \right| \le 1\] thì \[M\] chứa ít nhất 9 điểm.
Trường hợp với mọi \[P,Q\] sao cho \[PQ \ne 1\] và \[\left| {{M_P} \cap {M_Q}} \right| = 2\].
Khi đó \[{M_P} \cap {M_Q} = \left\{ {R;S} \right\}\], lúc đó \[{M_P} = \left\{ {R;S;T;U} \right\}\] và \[{M_Q} = \left\{ {R;S;V;W} \right\}\] và giả sử \[M = \left\{ {P;Q;R;S;T;U;V;W} \right\}\], ta có \[TQ \ne 1,{\rm{ }}UQ \ne 1,{\rm{ }}VP \ne 1,{\rm{ }}WP \ne 1\].
+ Nếu \[TR,TS,UR,US\] khác 1: \[{M_T} \cap {M_Q} = {M_U} \cap {M_Q} = \left\{ {V;W} \right\}\], suy ra \[T\] hay \[U\] trùng với \[Q\], vô lý.
+ Nếu \[TR,TS,UR,US\] có một số bằng 1: Không giảm đi tính tổng quát, giả sử \[TV{\rm{ }} = {\rm{ }}1\] lúc đó \[TS \ne 1\] và \[TV{\rm{ }} = {\rm{ }}1\] hay \(T{\rm{W}} = 1\). Giả sử \[TV{\rm{ }} = {\rm{ }}1\] lúc đó \[TW \ne 1\] suy ra \[TU{\rm{ }} = {\rm{ }}1\], và \[{M_T} = {\rm{ }}\left\{ {P;R;U;V} \right\}\] và \[{M_U} = \left\{ {P;T;V;W} \right\}\] lúc đó \[UTV,{\rm{ }}RPT,UTV\] là các tam giác đều cạnh 1, ta có hình bên. Điều này mâu thuẫn vì \[VR > 2\].
Vậy \[M\] chứa ít nhất là 9 điểm. Dấu bằng xảy ra với hình dưới.
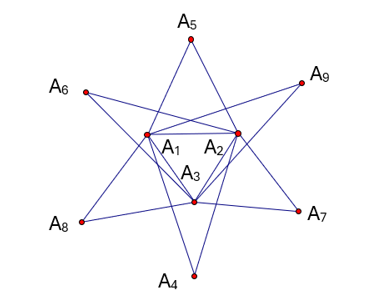
Vậy \[M\] có thể chứa ít nhất là 9 phần tử.
Đáp án cần nhập là: 9.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Khi ô tô dừng lại, ta có \(v\left( t \right) = 0 \Leftrightarrow - 2t + 20 = 0 \Leftrightarrow t = 10\).
Vậy từ thời điểm đạp phanh đến khi dừng lại, ô tô di chuyển được thêm 10 giây và quãng đường đi được là: \(s = \int\limits_0^{10} {\left( { - 2t + 20} \right)\,} dt = \left. {\left( { - {t^2} + 20t} \right)} \right|_0^{10} = 100\) (m).
Trong 5 giây trước đó, ô tô vẫn đang đi với vận tốc \(20\;{\rm{m}}/{\rm{s}}\) nên quãng đường đi được trong 5 giây này là: \(5 \cdot 20 = 100\)(m).
Vậy quãng đường mà ô tô đi được trong 15 giây cuối cùng bằng: \(100 + 100 = 200\;\,\left( {\rm{m}} \right)\).
Đáp án cần nhập là: \(200\).
Lời giải
Gọi số mol và số mol \[{C_4}{H_{10}}\] lần lượt là a và 2a, ta có: \[{C_3}{H_8}\]
44a + 58.2a = 12.1000 Þ a = 75 mol
Nhiệt đốt cháy 12 kg gas là Q = 75.2220 + 150.2874 = 597600 (kJ)
Số ngày sử dụng hết bình gas = \(\frac{{597600}}{{10000.\frac{{100}}{{80}}}} = 47,808 \approx 48\) (ngày)
Chọn A.Câu 3
A. \[\frac{{x - 2}}{3} = \frac{{y - 1}}{1} = \frac{{z - 4}}{{ - 2}}\]
B. \[\frac{{x + 3}}{1} = \frac{{y + 2}}{{ - 2}} = \frac{{z + 2}}{2}\].
C. \[\frac{{x - 3}}{1} = \frac{y}{{ - 2}} = \frac{{z - 2}}{2}\].
D. \[\frac{{x + 3}}{{ - 1}} = \frac{{y - 2}}{2} = \frac{{z + 2}}{{ - 2}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Hành chính công vụ.
B. Nghị luận.
C. Thuyết minh.
D. Tự sự.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Nhiệt độ trung bình tháng VII cao nhất ở Huế vì chịu tác động mạnh mẽ của gió phơn khô nóng.
B. Ở TP. Hồ Chí Minh, nhiệt độ tháng VII thấp hơn các địa điểm khác vì đây là tháng có mưa lớn.
C. Nhiệt độ trung bình năm tăng dần từ Bắc vào Nam vì càng về phía Nam góc nhập xạ càng lớn, lượng nhiệt nhận được càng nhiều.
D. Tháng I, chênh lệch nhiệt độ giữa 2 miền Bắc Nam rõ rệt do miền Bắc chịu ảnh hưởng của gió mùa Đông Nam lạnh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Tự sự.
B. Miêu tả.
C. Biểu cảm.
D. Nghị luận.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập