Một bình hình trụ có bán kính đáy là \({R_1} = 20\;{\rm{cm}}\) chứa nước ở nhiệt độ đặt trên mặt bàn nằm ngang. Người ta thả một quả cầu đặc bằng nhôm có bán kính \({{\rm{R}}_2} = 10\;{\rm{cm}}\) ở nhiệt độ vào bình thì khi cân bằng mực nước trong bình ngập chính giữa quả cầu, nhiệt độ của nước khi đó là t và độ lớn áp lực của quả cầu lên đáy bình là F . Đổ thêm dầu ở nhiệt độ vào bình cho vừa đủ ngập quả cầu thì nhiệt độ của hệ khi cân bằng nhiệt là \({t^\prime }\) và độ lớn áp lực của quả cầu lên đáy bình là \({{\rm{F}}^\prime }\). Bỏ qua sự trao đổi nhiệt giữa nước, quả cầu và dầu với bình và môi trường. Cho biết khối lượng riêng của nước, nhôm, dầu lần lượt là \({{\rm{D}}_1} = 1000\;{\rm{kg}}/{{\rm{m}}^3},{{\rm{D}}_2} = 2700\) \({\rm{kg}}/{{\rm{m}}^3}\) và \({{\rm{D}}_3} = 800\;{\rm{kg}}/{{\rm{m}}^3}\); nhiệt dung riêng của nước, nhôm và dầu lần lượt là \({{\rm{c}}_1} = 4200\;{\rm{J}}/{\rm{kgK}}\), \({{\rm{c}}_2} = 880\;{\rm{J}}/{\rm{kgK}}\ và \({{\rm{c}}_3} = 1800\;{\rm{J}}/{\rm{kgK}}\). Lấy \({\rm{g}} = 10\;{\rm{m}}/{{\rm{s}}^2}\).
Một bình hình trụ có bán kính đáy là \({R_1} = 20\;{\rm{cm}}\) chứa nước ở nhiệt độ đặt trên mặt bàn nằm ngang. Người ta thả một quả cầu đặc bằng nhôm có bán kính \({{\rm{R}}_2} = 10\;{\rm{cm}}\) ở nhiệt độ vào bình thì khi cân bằng mực nước trong bình ngập chính giữa quả cầu, nhiệt độ của nước khi đó là t và độ lớn áp lực của quả cầu lên đáy bình là F . Đổ thêm dầu ở nhiệt độ vào bình cho vừa đủ ngập quả cầu thì nhiệt độ của hệ khi cân bằng nhiệt là \({t^\prime }\) và độ lớn áp lực của quả cầu lên đáy bình là \({{\rm{F}}^\prime }\). Bỏ qua sự trao đổi nhiệt giữa nước, quả cầu và dầu với bình và môi trường. Cho biết khối lượng riêng của nước, nhôm, dầu lần lượt là \({{\rm{D}}_1} = 1000\;{\rm{kg}}/{{\rm{m}}^3},{{\rm{D}}_2} = 2700\) \({\rm{kg}}/{{\rm{m}}^3}\) và \({{\rm{D}}_3} = 800\;{\rm{kg}}/{{\rm{m}}^3}\); nhiệt dung riêng của nước, nhôm và dầu lần lượt là \({{\rm{c}}_1} = 4200\;{\rm{J}}/{\rm{kgK}}\), \({{\rm{c}}_2} = 880\;{\rm{J}}/{\rm{kgK}}\ và \({{\rm{c}}_3} = 1800\;{\rm{J}}/{\rm{kgK}}\). Lấy \({\rm{g}} = 10\;{\rm{m}}/{{\rm{s}}^2}\).
a) Giá trị của t gần bằng
b) Giá trị F gần bằng 92 N
c) Giá trị \({{\rm{t}}^\prime }\) gần bằng
Quảng cáo
Trả lời:
Thể tích quả cầu là \({V_2} = \frac{4}{3}\pi R_2^3 = \frac{4}{3}\pi \cdot {10^3}\;{\rm{c}}{{\rm{m}}^3} = \frac{4}{3}\pi \cdot {10^{ - 3}}\;{{\rm{m}}^3}\)
Khối lượng quả cầu là \({m_2} = {D_2}{V_2} = 2700 \cdot \frac{4}{3}\pi \cdot {10^{ - 3}} = 3,6\pi (\;{\rm{kg}})\)
Thể tích nước là \({V_1} = \pi R_1^2{R_2} - \frac{1}{2}{V_2} = \pi \cdot {20^2} \cdot 10 - \frac{1}{2} \cdot \frac{4}{3}\pi \cdot {10^3} = \frac{8}{3}\pi \cdot {10^3}\;{\rm{c}}{{\rm{m}}^3} = \frac{{10}}{3}\pi \cdot {10^{ - 3}}\;{{\rm{m}}^3}\)
Khối lượng nước là \({m_1} = {D_1}{V_1} = 1000 \cdot \frac{{10}}{3}\pi \cdot {10^{ - 3}} = \frac{{10}}{3}\pi (\;{\rm{kg}})\)
Phương trình cân bằng nhiệt:
a) Đúng \(F = P - {F_a} = mg - {D_1} \cdot \frac{1}{2}{V_2} \cdot g = 3,6\pi \cdot 10 - 1000 \cdot \frac{1}{2} \cdot \frac{4}{3}\pi \cdot {10^{ - 3}} \cdot 10 \approx 92N \Rightarrow \) b) Đúng
Khối lượng dầu là \({m_3} = {D_3}{V_3} = 800 \cdot \frac{{10}}{3}\pi \cdot {10^{ - 3}} = \frac{8}{3}\pi (\;{\rm{kg}})\)
Phương trình cân bằng nhiệt: \(3,6\pi \cdot 880 \cdot \left( {40 - {t^\prime }} \right) = \frac{{10\pi }}{3} \cdot 4200 \cdot \left( {{t^\prime } - 20} \right) + \frac{{8\pi }}{3} \cdot 1800 \cdot \left( {{t^\prime } - 15} \right)\)
c) Sai
\({F^\prime } = P - F_a^\prime = mg - \left( {{D_1} + {D_2}} \right) \cdot \frac{1}{2}{V_2} \cdot g = 3,6\pi \cdot 10 - (1000 + 800) \cdot \frac{1}{2} \cdot \frac{4}{3}\pi \cdot {10^{ - 3}} \cdot 10 \approx 75,4N\)
\( \Rightarrow \) d) ĐúngHot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
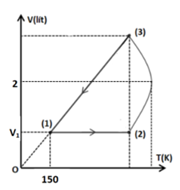
a) Áp suất khí ở trạng thái 3 gấp 3 lần áp suất khí ở trạng thái 1 .
b) Áp suất lớn nhất trong cả chu trình bằng áp suất ở trạng thái 2.
c) Nhiệt độ lớn nhất của chu trình bằng 600 K .
Lời giải
Áp suất khí ở trạng thái 3 bằng áp suất khí ở trạng thái \(1 \Rightarrow \) a) Sai
\(\frac{{pV}}{T} = nR \Rightarrow V = \frac{{nR}}{p} \cdot T \Rightarrow \) hệ số góc \(\frac{{nR}}{p}\) nhỏ nhất thì \(p\) lớn nhất \[ \Rightarrow \] b) Đúng c) Đúng
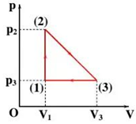
Theo Viet có \({V_1} + {V_3} = - \frac{b}{a} = - \frac{{600}}{{( - 150)}} = 4 \Rightarrow {V_1} = 4 - {V_3}\)
(3) sang (1) là đẳng áp \( \Rightarrow \frac{{{V_1}}}{{{T_1}}} = \frac{{{V_3}}}{{{T_3}}}\)
\( \Rightarrow \frac{{{V_1}}}{{150}} = \frac{{{V_3}}}{{600{V_3} - 150V_3^2}} \Rightarrow \frac{{4 - {V_3}}}{{150}} = \frac{1}{{600 - 150{V_3}}} \Rightarrow {V_3} = 3l \Rightarrow {V_1} = 1l\)
Quá trình \(2 \to 3\) có \(p = \frac{{nRT}}{V} = \frac{{R.\left( {600\;{\rm{V}} - 150\;{{\rm{V}}^2}} \right)}}{V} = (600 - 150\;{\rm{V}})R\) là hàm bậc nhất \( \Rightarrow {p_2} = (600 - 150.1)R = 450R\) và \({p_3} = (600 - 150.3)R = 150R\)
\({A^\prime } = \frac{1}{2}\left( {{p_2} - {p_3}} \right)\left( {{V_3} - {V_1}} \right) = \frac{1}{2} \cdot (450 - 150) \cdot R \cdot (3 - 1) = 300R \approx 2,49 \cdot {10^3}J \Rightarrow \)d) Sai
Câu 2
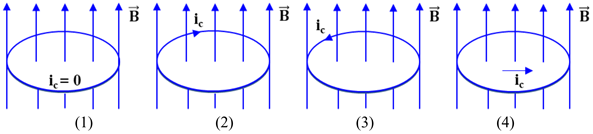
A. (1).
Lời giải
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
a) Hằng số phóng xạ của \(_{38}^{90}{\rm{Sr}}\) là \(0,024\;{{\rm{s}}^{ - 1}}\).
b) Độ phóng xạ của lượng \(_{38}^{90}{\rm{Sr}}\) có khối lượng \(0,0145\mu \;{\rm{g}}\) là 74 kBq .
c) Khối lượng \(_{38}^{90}{\rm{Sr}}\) tích tụ trong xương sẽ giảm \(20\% \) sau thời gian 15 năm.
1 . Tại thời điểm \({t_2} = 4,2{t_1}\), tỉ số giữa số hạt nhân X trong xương và số hạt nhân \(_{38}^{90}{\rm{Sr}}\) còn lại là
3. Tỉ số giữa số hạt nhân Strontium \(_{38}^{90}{\rm{Sr}}\) và số hạt nhân X ban đầu là 0,16
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(139,5{\rm{KJ}}\)
B. \(22,5{\rm{KJ}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.