PHẦN II. TỰ LUẬN
Cho biểu thức \(B = \frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} + \frac{4}{{1 - {x^2}}}.\)
a) Viết điều kiện xác định của biểu thức \[B.\]
b) Chứng minh \(B = \frac{4}{{x + 1}}\) và tính giá trị của biểu thức \[B\] tại \(x = - \frac{1}{2}.\)
c) Tìm các số nguyên \[x\] để giá trị của biểu thức \[B\] là số nguyên.
PHẦN II. TỰ LUẬN
Cho biểu thức \(B = \frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} + \frac{4}{{1 - {x^2}}}.\)
a) Viết điều kiện xác định của biểu thức \[B.\]
b) Chứng minh \(B = \frac{4}{{x + 1}}\) và tính giá trị của biểu thức \[B\] tại \(x = - \frac{1}{2}.\)
c) Tìm các số nguyên \[x\] để giá trị của biểu thức \[B\] là số nguyên.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) Ta có \(1 - {x^2} = - \left( {{x^2} - 1} \right) = - \left( {x - 1} \right)\left( {x + 1} \right).\)
Khi đó, điều kiện xác định của biểu thức \(B\) là \(\left\{ \begin{array}{l}x - 1 \ne 0\\x + 1 \ne 0\\1 - {x^2} \ne 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x - 1 \ne 0\\x + 1 \ne 0\\ - \left( {x - 1} \right)\left( {x + 1} \right) \ne 0\end{array} \right.,\) tức là \(\left\{ \begin{array}{l}x \ne 1\\x \ne - 1\end{array} \right..\)
Vậy để \(B\) xác định thì \(x \ne 1\) và \(x \ne - 1.\)
b) Với \(x \ne 1\) và \(x \ne - 1\) ta có:
\(B = \frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} + \frac{4}{{1 - {x^2}}}\)\( = \frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} - \frac{4}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)
\( = \frac{{{{\left( {x + 1} \right)}^2} - {{\left( {x - 1} \right)}^2} - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)\( = \frac{{\left( {{x^2} + 2x + 1} \right) - \left( {{x^2} - 2x + 1} \right) - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)
\( = \frac{{4x - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)\( = \frac{{4\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)\( = \frac{4}{{x + 1}}\).
Vì vậy với \(x \ne 1\) và \(x \ne - 1\) thì \(B = \frac{4}{{x + 1}}.\)
Với \(x = - \frac{1}{2}\) thoả mãn điều kiện xác định, thay vào biểu thức \(B = \frac{4}{{x + 1}},\) ta được:
\(B = \frac{4}{{ - \frac{1}{2} + 1}} = \frac{4}{{\frac{1}{2}}} = 8.\)
Vậy với \(x = - \frac{1}{2}\) thì \(B = 8.\)
c) Với \(x \ne 1\) và \(x \ne - 1\) thì \(B = \frac{4}{{x + 1}}.\)
Với \(x\) là số nguyên, để \(B\) nhận giá trị nguyên thì \(x + 1\) là ước của \(4.\)
Mà Ư\(\left( 4 \right) = \left\{ {1;\,\, - 1;\,\,2;\,\, - 2;\,\,4;\,\, - 4} \right\}.\)
Ta có bảng sau:
|
\(x + 1\) |
\(1\) |
\( - 1\) |
\(2\) |
\( - 2\) |
\(4\) |
\( - 4\) |
|
\(x\) |
\(0\) |
\( - 2\) |
\(1\) |
\( - 3\) |
\(3\) |
\( - 5\) |
Do đó: \(x \in \left\{ { - 5;\,\, - 3;\,\, - 2;\,\,0;\,\,1;\,\,3} \right\}.\)
Mà \(x \ne 1\) và \(x \ne - 1\) nên \(x \in \left\{ { - 5;\,\, - 3;\,\, - 2;\,\,0;\,\,3} \right\}.\)
Vậy để \(B\) nhận giá trị nguyên thì \(x \in \left\{ { - 5;\,\, - 3;\,\, - 2;\,\,0;\,\,3} \right\}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
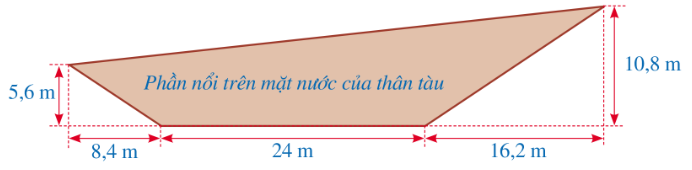
1) Giả sử mặt cắt dọc phần nổi trên mặt nước cả tàu thủy được mô tả như hình vẽ dưới đây:
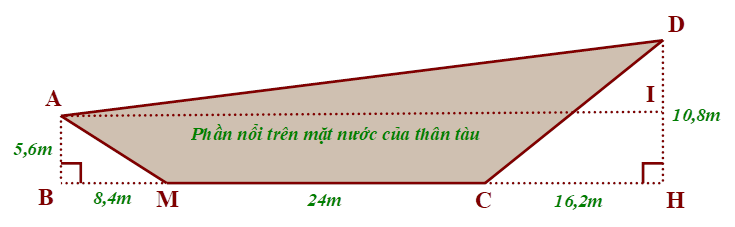
• Do tam giác \[ABM\] vuông tại \(B,\) nên theo định lí Pythagore ta có:
\[A{M^2} = A{B^2} + B{M^2} = {5,6^2} + {8,4^2} = 31,36 + 70,56 = 101,92\]
Suy ra \(AB = \sqrt {101,92} \,\,\left( {\rm{m}} \right).\)
• Do tam giác \(CDH\) vuông tại \(H,\) nên theo định lí Pythagore ta có:
\[C{D^2} = C{H^2} + D{H^2} = {16,2^2} + {10,8^2} = 262,44 + 116,64 = 379,08\]
Suy ra \(CD = \sqrt {379,08} \,\,\left( {\rm{m}} \right)\).
• Ta có \[AI = BH = BM + MC + CH = 8,4 + 24 + 16,2 = 48,6\] (m).
\[DI = DH--HI = DH--AB = 10,8--5,6 = 5,2\] (m).
Do tam giác \[ADI\] vuông tại \[I,\] nên theo định lí Pythagore ta có:
\[A{D^2} = A{I^2} + D{I^2} = {48,6^2} + {5,2^2} = 2{\rm{ }}361,96 + 27,04 = 2{\rm{ }}389\]
Suy ra \(AD = \sqrt {2\,389} \,\,\left( {\rm{m}} \right)\).
• Chu vi tứ giác \(AMCD\) là:
\[AM + MC + CD + DA = \]\(\sqrt {101,92} + 24 + \sqrt {379,08} + \sqrt {2389} \approx 102,4\) (m).
Vậy chu vi mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thuỷ đó khoảng \[102,4{\rm{\;m}}{\rm{.}}\]
2)
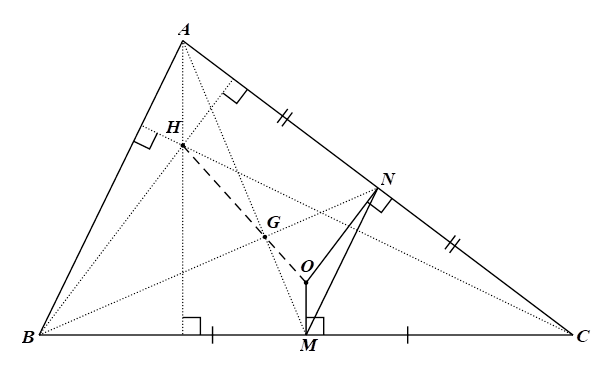
a) Vì \(O\) là giao điểm ba đường trung trực nên \(OM \bot AB.\)
Lại có \(AH \bot BC\) \((H\) là trực tâm) nên \(AH\,{\rm{//}}\,OM.\)
Tương tự, \(BH\,{\rm{//}}\,ON.\)
Do đó \(\widehat {MON} = \widehat {AHB}\) (hai góc tạo bởi hai đường thẳng song song)
Xét tam giác \[BAC\] có \(M,\,\,N\) lần lượt là trung điểm của \(BC\) và \(AC.\)
Do đó \(MN\) là đường trung bình của tam giác \(ABC\) nên \(MN\,{\rm{//}}\,AB,\) \(MN = \frac{1}{2}AB.\)
Suy ra \(\widehat {OMN} = \widehat {HAB}\) (hai góc tạo bởi hai đường thẳng song song)
Xét \(\Delta OMN\) và \(\Delta HAB\) có:
\(\widehat {MON} = \widehat {AHB}\) và \(\widehat {OMN} = \widehat {HAB}\)
Do đó (g.g).
b) Vì (câu a) nên (tỉ số cạnh tương ứng)
Vì \(G\) là trọng tâm của \(\Delta ABC,\) \(AM\) là trung tuyến nên \(\frac{{AG}}{{GM}} = 2,\) hay \(\frac{{GM}}{{AG}} = \frac{1}{2}\) \(\left( 2 \right)\)
Từ \(\left( 1 \right);\,\,\left( 2 \right)\) suy ra \(\frac{{GM}}{{AG}} = \frac{{OM}}{{AH}}.\)
Xét \(\Delta GOM\) và \(\Delta GHA\) có:
\(\frac{{GM}}{{AG}} = \frac{{OM}}{{AH}}\) và \(\widehat {OMG} = \widehat {HAG}\) (so le trong của \(AH\,{\rm{//}}\,OM)\)
Do đó (c.g.c).
c) Vì (câu b) nên (hai góc tương ứng).
Mà \(\widehat {HGM} + \widehat {HGA} = 180^\circ \) (kề bù) nên \[\widehat {HGM} + \widehat {OGM} = 180^\circ .\]
Do đó 3 điểm \(O;\,\,G;\,\,H\) thẳng hàng.
Mặt khác, nên \(\frac{{GO}}{{GH}} = \frac{{GM}}{{GA}} = \frac{1}{2},\) suy ra \(GH = 2GO.\)
Lời giải
Hướng dẫn giải
Gọi \(x\) là chữ số hàng chục của số cần tìm \((x \in \mathbb{N}\) và \(0 < x \le 9).\)
Khi đó chữ số hàng đơn vị là: \(12 - x.\)
Độ lớn số ban đầu là: \[10x + \left( {12 - x} \right).\]
Khi đổi chỗ hai chữ số đó cho nhau thì số mới có chữ số hàng chục là: \(12 - x\) và chữ số hàng đơn vị là \(x.\) Số mới có độ lớn là: \(10\left( {12 - x} \right) + x.\)
Sau khi đổi chỗ thì số mới bé hơn số ban đầu là 18 đơn vị nên ta có phương trình:
\(\left[ {10x + \left( {12 - x} \right)} \right] - \left[ {10\left( {12 - x} \right) + x} \right] = 18\)
\(10x + 12 - x - 120 + 10x - x = 18\)
\[10x - x + 10x - x = 18 - 12 + 120\]
\(18x = 126\)
\(x = 7\) (thỏa mãn).
Khi số cần tìm có chữ số hàng chục là 7 và chữ số hàng đơn vị là \(12 - 7 = 5.\)
Vậy số cần tìm là: 75.
Câu 3
A. \(12{\rm{\;cm}}.\)
B. \(14{\rm{\;cm}}.\)
C. \(16{\rm{\;cm}}.\)
D. \(18{\rm{\;cm}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[x - 1.\]
B. \[x + 1.\]
C. \[{x^2} - 1.\]
D. 35.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{{x + y}}{{{x^2} - xy}}.\)
B. \(\frac{{2x + y}}{{8{x^3} - 1}}.\)
C. \(\frac{{x + 8}}{{2:x}}.\)
D. \({x^2} + 2xy + {y^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập