Bác bảo vệ theo dõi số khách đến cơ quan mỗi ngày trong một tháng. Kết quả thu được như bảng sau:
Số khách
0
1
2
3
4
5
6
7
Số ngày
3
6
5
9
3
2
1
1
a) Gọi A là biến cố “Trong một ngày có từ 3 khách trở lên đến cơ quan”. Hỏi có bao nhiêu ngày biến cố A xảy ra?
b) Tính xác suất thực nghiệm của biến cố A.
c) Hãy ước lượng xác suất của biến cố B: “Trong một ngày có số khách đến cơ quan là số lẻ”.
Bác bảo vệ theo dõi số khách đến cơ quan mỗi ngày trong một tháng. Kết quả thu được như bảng sau:
|
Số khách |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Số ngày |
3 |
6 |
5 |
9 |
3 |
2 |
1 |
1 |
a) Gọi A là biến cố “Trong một ngày có từ 3 khách trở lên đến cơ quan”. Hỏi có bao nhiêu ngày biến cố A xảy ra?
b) Tính xác suất thực nghiệm của biến cố A.
c) Hãy ước lượng xác suất của biến cố B: “Trong một ngày có số khách đến cơ quan là số lẻ”.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
a) Theo bảng thống kê, số ngày có từ 3 khách trở lên đến cơ quan là:
\(9 + 3 + 2 + 1 + 1 = 16\) (ngày).
b) Số ngày bác bảo vệ theo dõi là: \(3 + 6 + 5 + 9 + 3 + 2 + 1 + 1 = 30\) (ngày).
Xác suất thực nghiệm của biến cố A là: \(P\left( A \right) = \frac{{16}}{{30}} = \frac{8}{{15}}.\)
c) Theo bảng thống kê, số ngày có khách đến cơ quan là số lẻ là \(6 + 9 + 2 + 1 = 18\) (ngày)
Xác suất thực nghiệm của biến cố B là \(P\left( B \right) = \frac{{18}}{{30}} = \frac{3}{5} = 60\% .\)
Vậy xác suất của biến cố B được ước lượng là \(60\% .\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Tổ Cường có 3 bạn nam và 1 bạn nữ tham gia vào câu lạc bộ thể thao, nên xác suất của biến cố “Bạn được chọn có tham gia câu lạc bộ thể thao” là \(\frac{{3 + 1}}{{13}} = \frac{4}{{13}}.\)Lời giải
Hướng dẫn giải
1) a) Bạn An có thể thu thập bằng phương pháp trực tiếp.
b) Dữ liệu thu được thuộc loại dữ liệu số.
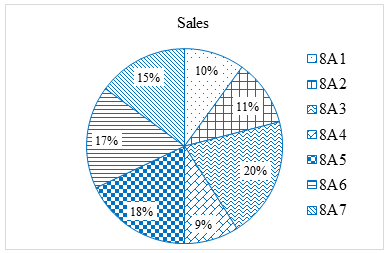
2) a) Số học sinh nữ lớp 8A1 là: \(100 \cdot 10\% = 10\) (học sinh).
Tương tự, ta tính được số học sinh nữ lớp 8A2, 8A3, 8A4, 8A5, 8A6, 8A7 lần lượt là: \(11;\,\,20;\,\,9;\,\,18;\,\,17;\,\,15\) học sinh.
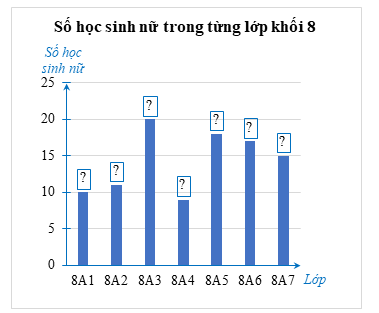
Bảng thống kê thể hiện số học sinh nữ trong từng lớp của khối 8 như sau:
|
Lớp |
8A1 |
8A2 |
8A3 |
8A4 |
8A5 |
8A6 |
8A7 |
|
Số học sinh nữ |
\(10\) |
\(11\) |
\(20\) |
\(9\) |
\(18\) |
\(17\) |
\(15\) |
Ta hoàn thành được biểu đồ cột như sau:
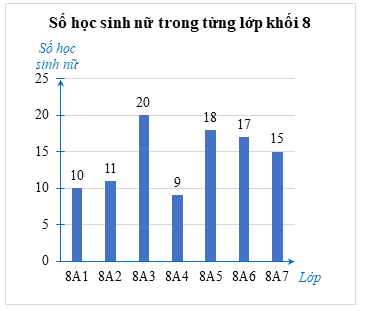
b) Biểu đồ đoạn thẳng thể hiện bảng thống kê ở câu a như sau:
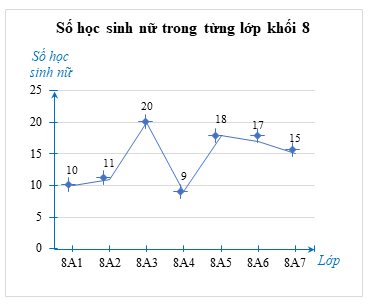
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.