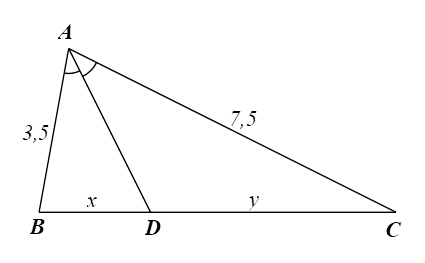Cho \(\Delta ABC,\) trung tuyến \[AM,\] đường phân giác của \(\widehat {AMB}\) cắt \[AB\] ở \[D,\] đường phân giác của \(\widehat {AMC}\) cắt \[AC\] ở \[E.\]
a) Chứng minh rằng \(AD \cdot AC = AE \cdot AB\) và \[DE\,{\rm{//}}\,BC.\]
b) Gọi \[I\] là giao điểm của \[AM\] và \[DE.\] Chứng minh rằng \(I\) là trung điểm của \(DE.\)
c) Tính \[DE,\] biết \[BC = 30{\rm{\;cm}}\] và \[AM = 10{\rm{\;cm}}.\]
d) Tam giác \[ABC\] phải thêm điều kiện gì để \(DE\) là đường trung bình của tam giác đó?
Cho \(\Delta ABC,\) trung tuyến \[AM,\] đường phân giác của \(\widehat {AMB}\) cắt \[AB\] ở \[D,\] đường phân giác của \(\widehat {AMC}\) cắt \[AC\] ở \[E.\]
a) Chứng minh rằng \(AD \cdot AC = AE \cdot AB\) và \[DE\,{\rm{//}}\,BC.\]
b) Gọi \[I\] là giao điểm của \[AM\] và \[DE.\] Chứng minh rằng \(I\) là trung điểm của \(DE.\)
c) Tính \[DE,\] biết \[BC = 30{\rm{\;cm}}\] và \[AM = 10{\rm{\;cm}}.\]
d) Tam giác \[ABC\] phải thêm điều kiện gì để \(DE\) là đường trung bình của tam giác đó?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
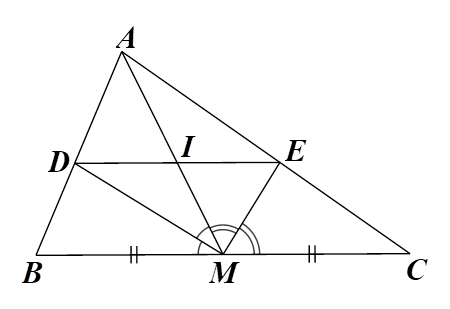
a) Xét \(\Delta ABM\) có \(MD\) là đường phân giác của \(\widehat {AMB}\) nên \(\frac{{MA}}{{MB}} = \frac{{DA}}{{DB}}\) \(\left( 1 \right)\) (tính chất đường phân giác của tam giác).
Xét \[\Delta ACM\] có \(ME\) là đường phân giác của \(\widehat {AMC}\) nên \(\frac{{MA}}{{MC}} = \frac{{EA}}{{EC}}\) \(\left( 2 \right)\) (tính chất đường phân giác của tam giác).
Do \(AM\) là đường trung tuyến của \[\Delta ABC\] nên \(M\) là trung điểm của \(BC,\) hay \(MB = MC = \frac{1}{2}BC.\,\,\,\left( 3 \right)\)
Từ \(\left( 1 \right),\,\,\left( 2 \right)\) và \(\left( 3 \right)\) ta có \(\frac{{DA}}{{DB}} = \frac{{EA}}{{EC}}.\)
Theo tính chất tỉ lệ thức ta có \(\frac{{DA}}{{DA + DB}} = \frac{{EA}}{{EA + EC}},\) hay \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}},\) suy ra \(AD \cdot AC = AE \cdot AB.\)
Xét \[\Delta ABC\] có \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}},\) theo định lí Thalès đảo ta có \[DE\,{\rm{//}}\,BC.\]
b) Xét \(\Delta ABM\) có \(DI\,{\rm{//}}\,BM,\) theo hệ quả định lí Thalès ta có \(\frac{{DI}}{{BM}} = \frac{{AI}}{{AM}}.\)
Xét \[\Delta ACM\] có \(IE\,{\rm{//}}\,MC,\) theo hệ quả định lí Thalès ta có \[\frac{{IE}}{{MC}} = \frac{{AI}}{{AM}}.\]
Do đó \(\frac{{DI}}{{BM}} = \frac{{IE}}{{MC}}.\)
Mà \(MB = MC\) (chứng minh ở câu a) nên \(DI = IE,\) hay \[I\] là trung điểm của \(DE.\)
c) Ta có \(MB = MC = \frac{1}{2}BC = \frac{1}{2} \cdot 30 = 15{\rm{\;cm}}.\)
Theo câu a, ta có \(\frac{{DA}}{{DB}} = \frac{{MA}}{{MB}},\) suy ra \[\frac{{DA}}{{DA + DB}} = \frac{{MA}}{{MA + MB}} = \frac{{10}}{{10 + 15}} = \frac{{10}}{{25}} = \frac{2}{5}.\]
Do đó \(\frac{{AD}}{{AB}} = \frac{2}{5}.\)
Xét \(\Delta ABC\) có \(DE\,{\rm{//}}\,BC,\) theo hệ quả định lí Thalès ta có \(\frac{{DE}}{{BC}} = \frac{{AD}}{{AB}} = \frac{2}{5}.\)
Suy ra \(DE = \frac{2}{5}BC = \frac{2}{5} \cdot 30 = 12{\rm{\;cm}}.\)
d) Để \(DE\) là đường trung bình của \(\Delta ABC\) thì \(D,\,\,E\) lần lượt là trung điểm của \(AB,\,\,AC.\)
Xét \(\Delta ABM\) có \(MD\) vừa là đường trung tuyến, vừa là đường phân giác nên là tam giác cân tại \(M.\) Suy ra \(MA = MB\) (tính chất tam giác cân).
Tương tự, ta cũng chứng minh được \(MA = MC.\)
Do đó \(MA = MB = MC = \frac{1}{2}BC.\)
Xét \(\Delta ABC\) có đường trung tuyến \(AM\) bằng nửa cạnh \(BC\) nên \(\Delta ABC\) vuông tại \(A.\)
Vậy \(\Delta ABC\) phải là tam giác vuông tại \(A\) thì \(DE\) là đường trung bình của tam giác đó.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Tổ Cường có 3 bạn nam và 1 bạn nữ tham gia vào câu lạc bộ thể thao, nên xác suất của biến cố “Bạn được chọn có tham gia câu lạc bộ thể thao” là \(\frac{{3 + 1}}{{13}} = \frac{4}{{13}}.\)Lời giải
Hướng dẫn giải
1) a) Bạn An có thể thu thập bằng phương pháp trực tiếp.
b) Dữ liệu thu được thuộc loại dữ liệu số.
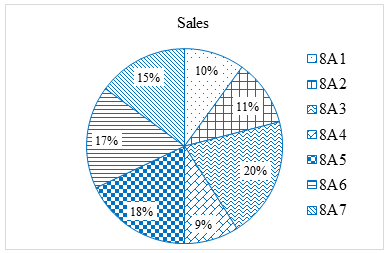
2) a) Số học sinh nữ lớp 8A1 là: \(100 \cdot 10\% = 10\) (học sinh).
Tương tự, ta tính được số học sinh nữ lớp 8A2, 8A3, 8A4, 8A5, 8A6, 8A7 lần lượt là: \(11;\,\,20;\,\,9;\,\,18;\,\,17;\,\,15\) học sinh.
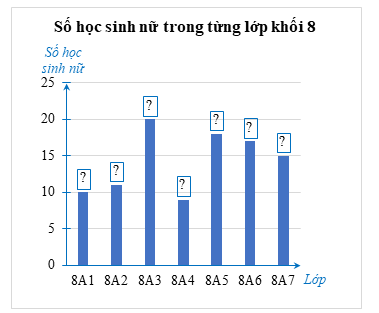
Bảng thống kê thể hiện số học sinh nữ trong từng lớp của khối 8 như sau:
|
Lớp |
8A1 |
8A2 |
8A3 |
8A4 |
8A5 |
8A6 |
8A7 |
|
Số học sinh nữ |
\(10\) |
\(11\) |
\(20\) |
\(9\) |
\(18\) |
\(17\) |
\(15\) |
Ta hoàn thành được biểu đồ cột như sau:
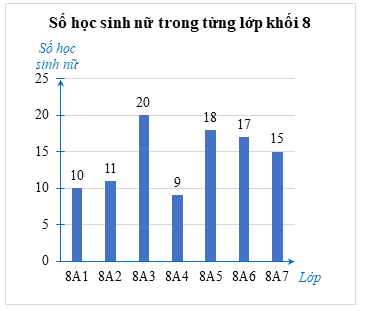
b) Biểu đồ đoạn thẳng thể hiện bảng thống kê ở câu a như sau:
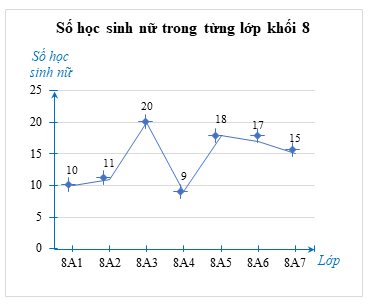
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.