1) Tìm độ dài \[x\] trong mỗi trường hợp sau:
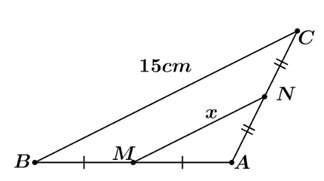
Hình 1
Hình 2
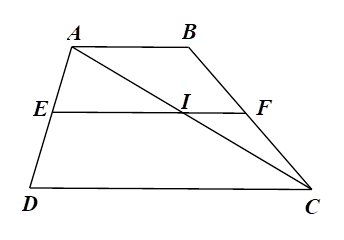
2) Cho hình thang \(ABCD\) có hai đáy \(AB\) và \(CD.\) Gọi \(M\) là trung điểm của \(CD,\) \(E\) là giao điểm của \(MA\) và \(BD,\) \(F\) là giao điểm của \(MB\) và \(AC.\)
a) Chứng minh rằng \[EF\,{\rm{//}}\,AB.\]
b) Đường thẳng \(EF\) cắt \(AD,\,\,BC\) lần lượt tại \(H\) và \(N.\)
i) Chứng minh \(HE = EF = FN.\)
ii) Biết \(AB = 7,5{\rm{\;cm}},\,\,CD = 12{\rm{\;cm}}.\) Tính độ dài \(HN.\)
1) Tìm độ dài \[x\] trong mỗi trường hợp sau:
|
Hình 1 |
Hình 2 |
2) Cho hình thang \(ABCD\) có hai đáy \(AB\) và \(CD.\) Gọi \(M\) là trung điểm của \(CD,\) \(E\) là giao điểm của \(MA\) và \(BD,\) \(F\) là giao điểm của \(MB\) và \(AC.\)
a) Chứng minh rằng \[EF\,{\rm{//}}\,AB.\]
b) Đường thẳng \(EF\) cắt \(AD,\,\,BC\) lần lượt tại \(H\) và \(N.\)
i) Chứng minh \(HE = EF = FN.\)
ii) Biết \(AB = 7,5{\rm{\;cm}},\,\,CD = 12{\rm{\;cm}}.\) Tính độ dài \(HN.\)
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
1)
|
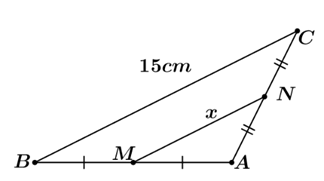
⦁ Hình 1: Tam giác \[ABC\] có \[M,\,\,N\] lần lượt là trung điểm của \[AB\] và \[AC\] nên \[MN\] là đường trung bình của tam giác. Do đó \[MN = \frac{1}{2}BC = \frac{1}{2} \cdot 15 = 7,5\,\,\left( {{\rm{cm}}} \right).\] Vậy \[x = 7,5\,\,{\rm{cm}}.\] |
Hình 1 |
|
|
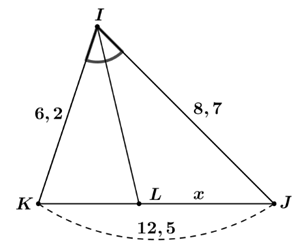
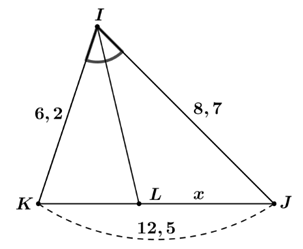
⦁ Hình 2: Xét tam giác \[IKJ\] có \[IL\] là phân giác trong góc \[\widehat {KIJ}\] (do \(\widehat {KIL} = \widehat {JIL}),\) nên \(\frac{{IK}}{{IJ}} = \frac{{LK}}{{LJ}}\) hay \[\frac{{LK}}{{IK}} = \frac{{LJ}}{{IJ}}\] Theo tính chất dãy tỉ số bằng nhau ta có: \[\frac{{LK}}{{6,2}} = \frac{{LJ}}{{8,7}} = \frac{{LK + LJ}}{{6,2 + 8,7}} = \frac{{KJ}}{{14,9}} = \frac{{12,5}}{{14,9}}.\] Suy ra \[LJ = \frac{{12,5}}{{14,9}} \cdot 8,7 \approx 7,3.\] |
 Hình 2 |
|
|
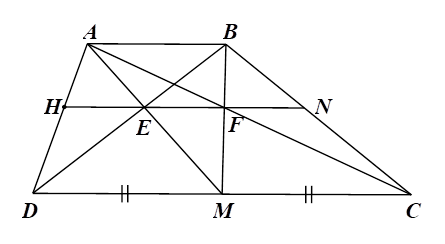
2) a) Vì \(ABCD\) là hình thang có hai đáy \(AB\) và \(CD\) nên \(AB\,{\rm{//}}\,CD.\) Vì \(AB\,{\rm{//}}\,DM\) (do \(AB\,{\rm{//}}\,CD),\) nên theo hệ quả định lí Thalès ta có \(\frac{{AE}}{{EM}} = \frac{{AB}}{{DM}}.\) \(\left( 1 \right)\) Vì \(AB\,{\rm{//}}\,MC\) (do \(AB\,{\rm{//}}\,CD),\) nên theo hệ quả định lí Thalès ta có \(\frac{{BF}}{{FM}} = \frac{{AB}}{{MC}}.\) \(\left( 2 \right)\) Lại có \(M\) là trung điểm của \(CD\) nên \(DM = MC.\) \(\left( 3 \right)\) Từ \(\left( 1 \right),\) \(\left( 2 \right)\) và \(\left( 3 \right)\) ta có \(\frac{{AE}}{{EM}} = \frac{{BF}}{{FM}},\) theo định lí Thalès đảo ta có \(EF\,{\rm{//}}\,AB.\) |
 |
|
b) i)Xét \(\Delta ADM\) có \(HE\,{\rm{//}}\,DM,\) theo hệ quả định lí Thalès ta có \(\frac{{HE}}{{DM}} = \frac{{AE}}{{AM}}.\)
Xét \(\Delta AMC\) có \(EF\,{\rm{//}}\,MC,\) theo hệ quả định lí Thalès ta có \[\frac{{EF}}{{MC}} = \frac{{AE}}{{AM}}.\]
Do đó \(\frac{{HE}}{{DM}} = \frac{{EF}}{{MC}},\) mà \(DM = MC\) nên \(HE = EF.\)
Chứng minh tương tự ta cũng có \(EF = FN.\) Suy ra \(HE = EF = FN.\)
ii) Vì \(M\) là trung điểm của \(CD\) nên \(DM = MC = \frac{1}{2}CD = \frac{1}{2} \cdot 12 = 6{\rm{\;cm}}.\)
Theo câu a, ta có \(\frac{{AE}}{{EM}} = \frac{{AB}}{{DM}} = \frac{{7,5}}{6} = \frac{5}{4}.\) Suy ra \(\frac{{AE}}{5} = \frac{{EM}}{4}.\)
Theo tính chất của dãy tỉ số bằng nhau ta có: \(\frac{{AE}}{5} = \frac{{EM}}{4} = \frac{{AE + EM}}{{5 + 4}} = \frac{{AM}}{9}.\)
Do đó \(\frac{{AE}}{{AM}} = \frac{5}{9}.\)
Mà theo câu b, \(\frac{{HE}}{{DM}} = \frac{{AE}}{{AM}} = \frac{5}{9}.\)
Suy ra \(HE = \frac{5}{9}DM = \frac{5}{9} \cdot 6 = \frac{{10}}{3}{\rm{\;cm}}.\)
Vậy \(HN = 3HE = 3 \cdot \frac{{10}}{3} = 10{\rm{\;cm}}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
![Biểu đồ dưới đây biểu diễn tỉ lệ hoa quả bán được trong một ngày của một cửa hàng. Biết ngày hôm đó cửa hàng bán được \[150\] kg hoa quả. Khẳng định nào sau đây là đúng? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid9-1768899350.png)
A. Cửa hàng bán được \[30\] kg táo.
B. Khối lượng nhãn bán được nhiều hơn khối lượng nho bán được là 30 kg.
C. Cửa hàng bán được tổng cộng \[45\] kg lê và nho.
D. Khối lượng nhãn bán được là \[40\] kg.
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Cửa hàng bán được số kg táo là: \(150 \cdot 30\% = 45\) (kg).
Tương tự, ta tính được khối lượng lê, nhãn, nho cửa hàng bán được lần lượt là: \(30\) kg; \(60\) kg; \(15\) kg.
Khối lượng nhãn bán được nhiều hơn khối lượng nho là \(50 - 15 = 45\) (kg).
Cửa hàng bán được tổng cộng \(30 + 15 = 45\) kg lê và nho.
Vậy ta chọn phương án C.
Lời giải
Hướng dẫn giải
a) Bảng thống kê:
|
Lớp Câu lạc bộ |
8A1 |
8A2 |
8A3 |
8A4 |
|
Cầu lông |
10 |
8 |
5 |
12 |
|
Cờ vua |
12 |
14 |
14 |
10 |
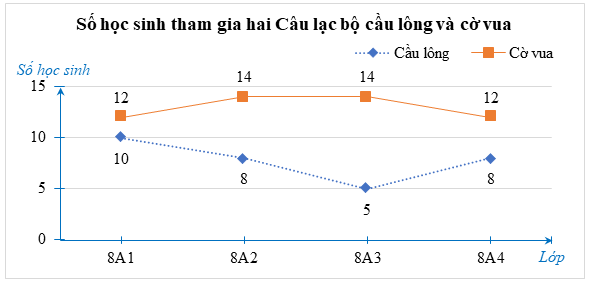
Ta vẽ vẽ biểu đồ cột kép để biểu diễn số lượng học sinh tham gia đăng kí hai Câu lạc bộ cầu lông và cờ vua của trường đó như sau:
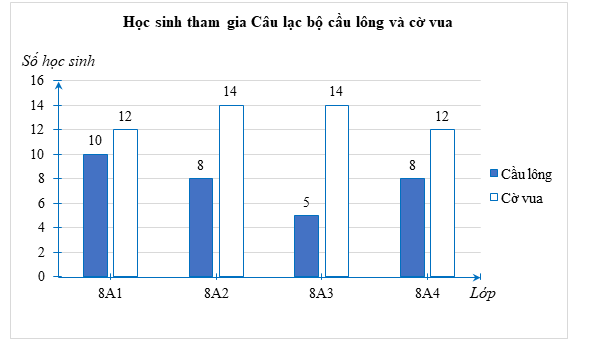
b) Vì số lượng tham gia Câu lạc bộ cầu lông của lớp 8A1 chiếm \(25\% \) tổng số học sinh cả lớp nên số học sinh của lớp 8A1 là: \(10:25\% = 40\) (học sinh).
c) ⦁ Lớp 8A3 đăng kí tham gia cầu lông ít hơn lớp 8A4 (ít hơn \(3\) bạn) và đăng kí tham gia cờ vua nhiều hơn lớp lớp 8A4 (nhiều hơn 2 bạn).
⦁ Tổng số học sinh tham gia Câu lạc bộ cầu lông là: \(10 + 8 + 5 + 12 = 35\) (học sinh).
Tổng số học sinh tham gia Câu lạc bộ cờ vua là: \(12 + 14 + 14 + 10 = 50\) (học sinh).
Vậy tổng số học sinh tham gia Câu lạc bộ cầu lông ít hơn tổng số học sinh tham gia Câu lạc bộ cờ vua.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{{AE}}{{ED}} = \frac{{AI}}{{IC}}.\)
B. \(\frac{{AE}}{{ED}} = \frac{{BF}}{{FC}}.\)
C. \(\frac{{AI}}{{AC}} = \frac{{EI}}{{DC}}.\)
D. \(\frac{{IC}}{{IA}} = \frac{{IF}}{{AB}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{2}{{33}}.\)
B. \(\frac{{16}}{{33}}.\)
C. \(\frac{{12}}{{33}}.\)
D. \(\frac{1}{{33}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(1,5{\rm{\;cm}}.\)
B. \(2{\rm{\;cm}}.\)
C. \(2,5{\rm{\;cm}}.\)
D. \(10{\rm{\;cm}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập