Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều có đáp án - Đề 05
29 người thi tuần này 4.6 424 lượt thi 9 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 09
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 08
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 07
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Danh sách câu hỏi:
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Tìm hiểu trên mạng Internet về số ca mắc bệnh COVID-19 ở Việt Nam là trường hợp thu thập dữ liệu gián tiếp.
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Cửa hàng bán được số kg táo là: \(150 \cdot 30\% = 45\) (kg).
Tương tự, ta tính được khối lượng lê, nhãn, nho cửa hàng bán được lần lượt là: \(30\) kg; \(60\) kg; \(15\) kg.
Khối lượng nhãn bán được nhiều hơn khối lượng nho là \(50 - 15 = 45\) (kg).
Cửa hàng bán được tổng cộng \(30 + 15 = 45\) kg lê và nho.
Vậy ta chọn phương án C.
Câu 3
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Xác suất lấy được quả bóng màu xanh là \(\frac{{12}}{{16 + 12 + 3 + 2}} = \frac{{12}}{{33}}.\)Câu 4
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
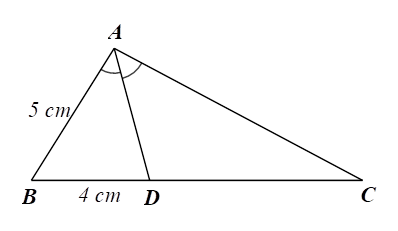
Xét \(\Delta ABC\) có \(AD\) là đường phân giác của góc \(BAC\) (do \(\widehat {BAD} = \widehat {CAD}),\) nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\) (tính chất đường phân giác).
Suy ra \(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}\) (tính chất tỉ lệ thức)
Do đó \(\frac{{AC}}{{CD}} = \frac{5}{4}.\)Câu 5
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
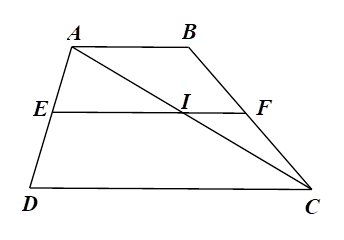
Xét \(\Delta ADC\) với \(EI\,{\rm{//}}\,DC\) ta có:
⦁ \(\frac{{AE}}{{ED}} = \frac{{AI}}{{IC}}\) (định lí Thalès). Do đó A là khẳng định đúng.
⦁ \(\frac{{AI}}{{AC}} = \frac{{EI}}{{DC}}\) (hệ quả của định lí Thalès). Do đó C là khẳng định đúng.
Xét \(\Delta ABC\) với \(IF\,{\rm{//}}\,AB\) ta có:
⦁ \(\frac{{AI}}{{IC}} = \frac{{BF}}{{FC}}\) (định lí Thalès).
Mà \(\frac{{AE}}{{ED}} = \frac{{AI}}{{IC}}\) nên \(\frac{{AE}}{{ED}} = \frac{{BF}}{{FC}}.\) Do đó A là khẳng định đúng.
⦁ \(\frac{{IC}}{{AC}} = \frac{{IF}}{{AB}}\) (hệ quả định lí Thalès). Do đó D là khẳng định sai.
Vậy ta chọn phương án D.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
1) Tìm độ dài \[x\] trong mỗi trường hợp sau:
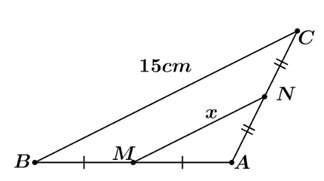
Hình 1
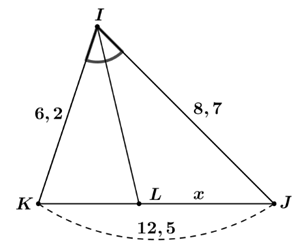
Hình 2
2) Cho hình thang \(ABCD\) có hai đáy \(AB\) và \(CD.\) Gọi \(M\) là trung điểm của \(CD,\) \(E\) là giao điểm của \(MA\) và \(BD,\) \(F\) là giao điểm của \(MB\) và \(AC.\)
a) Chứng minh rằng \[EF\,{\rm{//}}\,AB.\]
b) Đường thẳng \(EF\) cắt \(AD,\,\,BC\) lần lượt tại \(H\) và \(N.\)
i) Chứng minh \(HE = EF = FN.\)
ii) Biết \(AB = 7,5{\rm{\;cm}},\,\,CD = 12{\rm{\;cm}}.\) Tính độ dài \(HN.\)
1) Tìm độ dài \[x\] trong mỗi trường hợp sau:
|

Hình 1 |
 Hình 2 |
2) Cho hình thang \(ABCD\) có hai đáy \(AB\) và \(CD.\) Gọi \(M\) là trung điểm của \(CD,\) \(E\) là giao điểm của \(MA\) và \(BD,\) \(F\) là giao điểm của \(MB\) và \(AC.\)
a) Chứng minh rằng \[EF\,{\rm{//}}\,AB.\]
b) Đường thẳng \(EF\) cắt \(AD,\,\,BC\) lần lượt tại \(H\) và \(N.\)
i) Chứng minh \(HE = EF = FN.\)
ii) Biết \(AB = 7,5{\rm{\;cm}},\,\,CD = 12{\rm{\;cm}}.\) Tính độ dài \(HN.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Biểu đồ dưới đây biểu diễn tỉ lệ hoa quả bán được trong một ngày của một cửa hàng. Biết ngày hôm đó cửa hàng bán được \[150\] kg hoa quả. Khẳng định nào sau đây là đúng? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid9-1768899350.png)