Một xưởng sản xuất hàng thủ công mỹ nghệ, kiểm tra chất lượng của \[100\] sản phẩm. Kết quả được ghi trong bảng sau:
Số lỗi
0
1
\[ > 1\]
Số sản phẩm
78
20
2
Chọn ngẫu nhiên một sản phẩm của nhà máy. Xác suất thực nghiệm của biến cố “Sản phẩm có nhiều hơn 1 lỗi” là
Một xưởng sản xuất hàng thủ công mỹ nghệ, kiểm tra chất lượng của \[100\] sản phẩm. Kết quả được ghi trong bảng sau:
|
Số lỗi |
0 |
1 |
\[ > 1\] |
|
Số sản phẩm |
78 |
20 |
2 |
Chọn ngẫu nhiên một sản phẩm của nhà máy. Xác suất thực nghiệm của biến cố “Sản phẩm có nhiều hơn 1 lỗi” là
A. \[0,22.\]
B. \[0,78.\]
C. \[0,2.\]
D. \[0,02.\]
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D
Trong \[100\] sản phẩm được kiểm tra, có \[2\] sản phẩm có nhiều hơn 1 lỗi.
Xác suất thực nghiệm của biến cố “Sản phẩm có nhiều hơn 1 lỗi” là \[\frac{2}{{100}} = 0,02.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
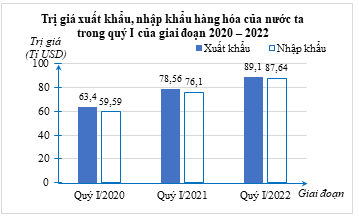
a) i) Ta lập được bảng thống kê như sau:
|
Giai đoạn |
Quý I/2020 |
Quý I/2021 |
Quý I/2022 |
|
Xuất khẩu |
\(63,4\) |
\(78,56\) |
\(89,1\) |
|
Nhập khẩu |
\(59,59\) |
\(76,1\) |
\(87,64\) |
|
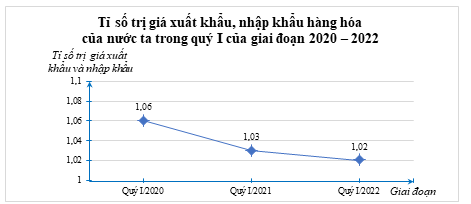
Tỉ số trị giá xuất khẩu và nhập khẩu |
\(\frac{{63,4}}{{59,59}} \approx 1,06\) |
\(\frac{{78,56}}{{76,1}} \approx 1,03\) |
\(\frac{{89,1}}{{87,64}} \approx 1,02\) |
ii) Biểu đồ đoạn thẳng biểu diễn tỉ số trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 – 2022 như sau:
b) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 – 2022 là \(63,4 + 78,56 + 89,1 = 231,06\) (tỉ USD).
c) Trị giá nhập khẩu hàng hóa của nước ta trong quý I năm 2022 tăng \(\frac{{87,64 - 76,1}}{{76,1}} \cdot 100\% \approx 15,16\% \) so với quý I năm 2021.
Lời giải
Hướng dẫn giải
|
1) a) Xét \(\Delta ABC\) có \(AB \bot AC;\,\,IN \bot AC\) nên \(AB\,{\rm{//}}\,IN.\) Mà \(I\) là trung điểm của \(BC\) nên \(IN\) là đường trung bình của tam giác, do đó \(N\) là trung điểm của \(AC.\) Xét tứ giác \(ADCI\) có: \(N\) là trung điểm của \(ID,\,\,AC\) nên \(ADCI\) là hình bình hành. Lại có \(IN \bot AC\) hay \(ID \bot AC\) nên hình bình hành \(ADCI\) là hình thoi.\(\)
|
 |
|
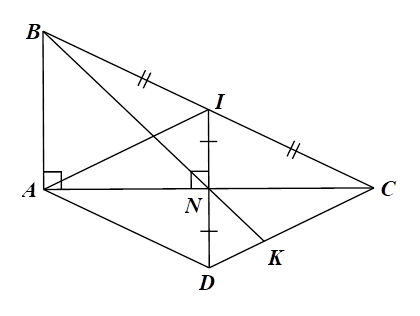b) Kẻ \(IH\,{\rm{//}}\,BK\,\,\left( {H \in CD} \right),\) mà \(I\) là trung điểm của \(BC,\) nên \(IH\) là đường trung bình của \(\Delta BKC.\) Do đó \(H\) là trung điểm của \(KC\) hay \(KH = HC\,\,\left( 1 \right)\) Xét \[\Delta DIH\] có \(N\) là trung điểm của \[DI\] và \[NK\,{\rm{//}}\,IH\] (do \[BK\,{\rm{//}}\,IH)\] nên \(NK\) là đường trung bình của \[\Delta DIH,\] suy ra \(K\)là trung điểm của \(DH\) hay \(DK = KH\,\,\left( 2 \right)\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(DK = KH = HC.\) Do đó \(\frac{{DK}}{{DC}} = \frac{1}{3}.\) |
 |
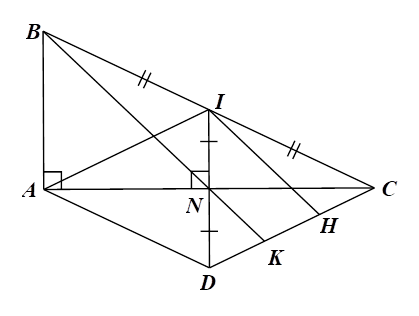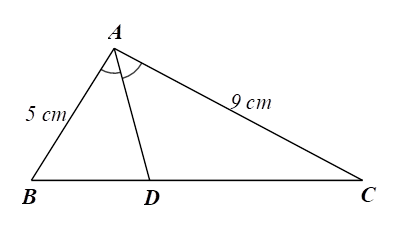
2) a) Trong \(\Delta ABD\) có: \[AM\] là phân giác của góc \(\widehat {BAD}\) nên \(\frac{{AB}}{{AD}} = \frac{{MB}}{{MD}}\) (tính chất đường phân giác trong tam giác).
Tương tự: trong \(\Delta ADC\) có \[DN\] là phân giác góc \(\widehat {ADC}\) nên \(\frac{{DC}}{{DA}} = \frac{{NC}}{{NA}}.\)
Mà \[AB = DC\] (do \[ABCD\] là hình bình hành) suy ra \(\frac{{AB}}{{AD}} = \frac{{MB}}{{MD}} = \frac{{NC}}{{NA}}.\)
b) Theo câu a, \(\frac{{MB}}{{MD}} = \frac{{NC}}{{NA}}\) suy ra \(\frac{{MB}}{{MD}} + 1 = \frac{{NC}}{{NA}} + 1\) hay \(\frac{{MB + MD}}{{MD}} = \frac{{NC + NA}}{{NA}}\)
Suy ra \(\frac{{BD}}{{MD}} = \frac{{AC}}{{NA}}\) \[\left( 1 \right)\]
Mà \[ABCD\] là hình bình hành nên hai đường chéo \[AC\] và \[BD\] cắt nhau tại trung điểm \[O\] của mỗi đường, suy ra \[BD = 2DO,\] \[AC = 2AO\] \[\left( 2 \right)\]
Từ (1) và (2) suy ra \[\frac{{2DO}}{{DM}} = \frac{{2AO}}{{AN}}\] hay \(\frac{{DO}}{{DM}} = \frac{{AO}}{{AN}}\)
Xét \(\Delta OAD\) có \(\frac{{DO}}{{DM}} = \frac{{AO}}{{AN}}\) nên \[MN\,{\rm{//}}\,AD\] (định lí Thalès đảo).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{5}{9}.\)
B. \(\frac{9}{5}.\)
C. \(\frac{5}{{14}}.\)
D. \[\frac{9}{{14}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{{MH}}{{MN}} = \frac{{MK}}{{MP}}.\)
B. \(\frac{{MH}}{{HN}} = \frac{{MK}}{{KP}}.\)
C. \(\frac{{NH}}{{MN}} = \frac{{MP}}{{KP}}.\)
D. \[\frac{{NH}}{{MN}} = \frac{{PK}}{{MP}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Dân số Trung Quốc luôn thấp hơn dân số Ấn Độ.
B. Dân số Trung Quốc luôn cao hơn dân số Ấn độ.
C. Hiện tại dân số Trung Quốc cao hơn nhưng sẽ thấp hơn dân số Ấn Độ trong tương lai.
D. Hiện tại dân số Trung Quốc thấp hơn nhưng sẽ cao hơn dân số Ấn Độ trong tương lai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Thời gian (đơn vị giờ) để hoàn thành bài tập về nhà: \[0,8;{\rm{ }}1;{\rm{ }}1,5;{\rm{ }}2.\]
B. Số hoạt động tình nguyện đã tham gia: \[0;{\rm{ }}1;{\rm{ }}1;{\rm{ }}3.\]
C. Số thành viên trong gia đình: \[4;{\rm{ }}4;{\rm{ }}3;{\rm{ }}5.\]
D. Số chữ cái trong tên: \[3;{\rm{ }}6;{\rm{ }}3;{\rm{ }}2.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập