PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một công ty thống kê tuổi của các nhân viên và kết quả được cho trong bảng số liệu ghép nhóm sau:
Nhóm
\[\left[ {23;26} \right)\]
\[\left[ {26;29} \right)\]
\[\left[ {29;32} \right)\]
\[\left[ {32;35} \right)\]
\[\left[ {35;38} \right)\]
Tần số
\[23\]
\[40\]
\[56\]
\[33\]
\[8\]
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần mười) là bao nhiêu?
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một công ty thống kê tuổi của các nhân viên và kết quả được cho trong bảng số liệu ghép nhóm sau:
|
Nhóm |
\[\left[ {23;26} \right)\] |
\[\left[ {26;29} \right)\] |
\[\left[ {29;32} \right)\] |
\[\left[ {32;35} \right)\] |
\[\left[ {35;38} \right)\] |
|
Tần số |
\[23\] |
\[40\] |
\[56\] |
\[33\] |
\[8\] |
Quảng cáo
Trả lời:
Đáp án:
Đáp án: \[4,8\].
|
Nhóm |
\[\left[ {23;26} \right)\] |
\[\left[ {26;29} \right)\] |
\[\left[ {29;32} \right)\] |
\[\left[ {32;35} \right)\] |
\[\left[ {35;38} \right)\] |
|
Tần số |
\[23\] |
\[40\] |
\[56\] |
\[33\] |
\[8\] |
|
Tần số tích luỹ |
\[23\] |
\[63\] |
\[119\] |
\[152\] |
\[160\] |
Có \[n = 160\]; \[\frac{n}{4} = 40\] và \[\frac{{3n}}{4} = 120\] nên nhóm chứa \[{Q_1};{Q_3}\] lần lượt là \[2;4\].
Do đó \[{Q_1} = 26 + \frac{{40 - 23}}{{40}}.\left( {29 - 26} \right) = \frac{{1\;091}}{{40}}\] và \[{Q_3} = 32 + \frac{{120 - 119}}{{33}}.\left( {35 - 32} \right) = \frac{{353}}{{11}}\]
Suy ra \[{\Delta _Q} = {Q_3} - {Q_1} = \frac{{353}}{{11}} - \frac{{1\;091}}{{40}} = \frac{{2119}}{{440}} \approx 4,8\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 0,83.
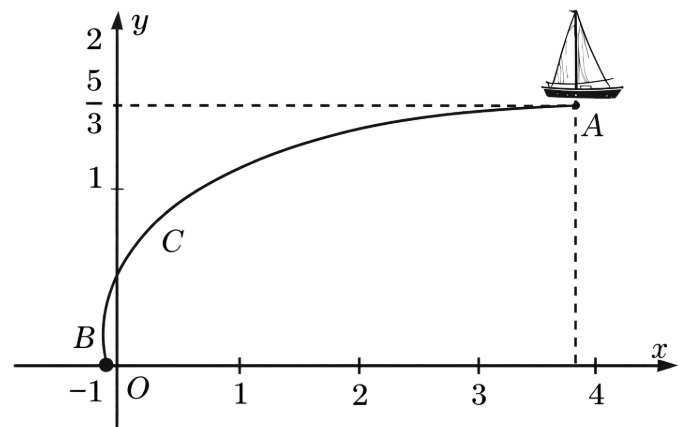
Gọi hàm số biểu diễn quỹ đạo chuyển động của thuyền là \(y = f(x) = \frac{{ax + b}}{{cx + d}}\).
Theo đề bài, cung đường \(AB\) là một phần của đồ thị hàm số này.
Điểm \(B( - 1;0)\) nằm trên đồ thị, nên: \(0 = \frac{{a( - 1) + b}}{{c( - 1) + d}} \Leftrightarrow - a + b = 0 \Leftrightarrow b = a\quad (1)\)
Điểm \(A\left( {4;\frac{5}{3}} \right)\) nằm trên đồ thị, nên: \(\frac{5}{3} = \frac{{a(4) + b}}{{c(4) + d}}\quad (2)\)
Từ \((1)\), thay \(b = a\) vào \((2)\):\(\frac{5}{3} = \frac{{4a + a}}{{4c + d}} = \frac{{5a}}{{4c + d}}\)\( \Leftrightarrow 5(4c + d) = 15a\)\( \Leftrightarrow 4c + d = 3a\quad (3)\)
Quan sát đồ thị, ta thấy đường cong đi qua điểm \((0;1)\) (điểm giao với trục \(Oy\)). Giả sử điểm \((0;1)\) nằm trên đồ thị, khi đó: \(1 = \frac{{a(0) + b}}{{c(0) + d}} \Leftrightarrow 1 = \frac{b}{d} \Leftrightarrow b = d\quad (4)\)
Từ \((1)\) và \((4)\), ta có \(a = b = d\).
Thay \(d = a\) vào \((3)\): \(4c + a = 3a\)\( \Leftrightarrow 4c = 2a\)\( \Leftrightarrow a = 2c\quad (5)\)
Để đơn giản, ta chọn \(c = 1\), từ \((5)\) suy ra \(a = 2\).
Khi đó \(b = a = 2\) và \(d = a = 2\). Vậy hàm số có dạng \(y = \frac{{2x + 2}}{{x + 2}}\).
Kiểm tra lại với các điểm đã cho:
Với \(B( - 1;0)\): \(y = \frac{{2( - 1) + 2}}{{ - 1 + 2}} = \frac{0}{1} = 0\). (Thỏa mãn)
Với \(A\left( {4;\frac{5}{3}} \right)\): \(y = \frac{{2(4) + 2}}{{4 + 2}} = \frac{{8 + 2}}{6} = \frac{{10}}{6} = \frac{5}{3}\). (Thỏa mãn)
Gọi \(M(x;y)\) là một điểm trên cung đường \(AB\). Khoảng cách từ \(M\) đến gốc tọa độ \(O(0;0)\) là \(OM = \sqrt {{{(x - 0)}^2} + {{(y - 0)}^2}} = \sqrt {{x^2} + {y^2}} \).
Để \(OM\) ngắn nhất, ta cần tìm giá trị nhỏ nhất của \(O{M^2} = S(x) = {x^2} + {y^2}\) với \(x \in [ - 1;4]\).
Thay \(y = \frac{{2x + 2}}{{x + 2}}\) vào \(S(x)\)ta được: \(S(x) = {x^2} + {\left( {\frac{{2x + 2}}{{x + 2}}} \right)^2}\).
Ta có: \(S'(x) = 2x + 2\left( {\frac{{2x + 2}}{{x + 2}}} \right) \cdot \left( {\frac{2}{{{{(x + 2)}^2}}}} \right) = 2x + \frac{{4(2x + 2)}}{{{{(x + 2)}^3}}} = 2x + \frac{{8x + 8}}{{{{(x + 2)}^3}}}\)
\(S'(x) = 0\)\( \Leftrightarrow 2x + \frac{{8x + 8}}{{{{(x + 2)}^3}}} = 0\)\( \Leftrightarrow {x^4} + 6{x^3} + 12{x^2} + 12x + 4 = 0\).
Trên đoạn \([ - 1;4]\), ta tìm được nghiệm thực của phương trình \({x^4} + 6{x^3} + 12{x^2} + 12x + 4 = 0\) là \({x_0} \approx - 0,5826\).
Tại \(x = - 1\) (điểm \(B\)): \(O{M^2} = {( - 1)^2} + {0^2} = 1\) \( \Rightarrow OM = 1\).
Tại \(x = 4\) (điểm \(A\)): \(O{M^2} = {4^2} + {\left( {\frac{5}{3}} \right)^2} = 16 + \frac{{25}}{9} = \frac{{144 + 25}}{9} = \frac{{169}}{9}\)\( \Rightarrow OM = \sqrt {\frac{{169}}{9}} = \frac{{13}}{3} \approx 4,333\).
Tại \({x_0} \approx - 0.5826\), ta có: \({y_0} = \frac{{2{x_0} + 2}}{{{x_0} + 2}} = \frac{{2 \cdot \left( { - 0,5826} \right) + 2}}{{ - 0,5826 + 2}} = \frac{{ - 1,1652 + 2}}{{1,4174}} = \frac{{0,8348}}{{1,4174}} \approx 0,58896\).
\(OM = \sqrt {x_0^2 + y_0^2} = \sqrt {{{\left( { - 0,5826} \right)}^2} + {{\left( {0,58896} \right)}^2}} \)
\(OM = \sqrt {0,33942076 + 0,34687392} = \sqrt {0,68629468} \approx 0,82842\).
So sánh các giá trị \(OM\) tìm được giá trị nhỏ nhất là \(0,82842\).
Làm tròn kết quả đến hàng phần trăm, ta được \(0,83\).
Lời giải
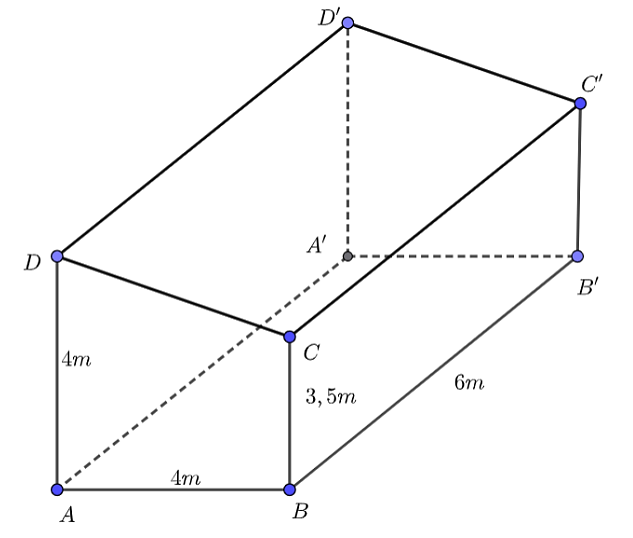
Ta trải phẳng 3 mặt phẳng \(\left( {ADD'A'} \right)\), \(\left( {A'B'C'D'} \right)\) và \(\left( {CBB'C'} \right)\) như hình vẽ bên dưới.
Khi đó muốn nối dây điện từ bảng điểu khiển men theo các bức tường (không mắc lên mái) đến 2 bóng điện trên ngắn nhất thì độ dài của \(M{D_1} + M{D_2}\) ngắn nhất như hình vẽ bên dưới.
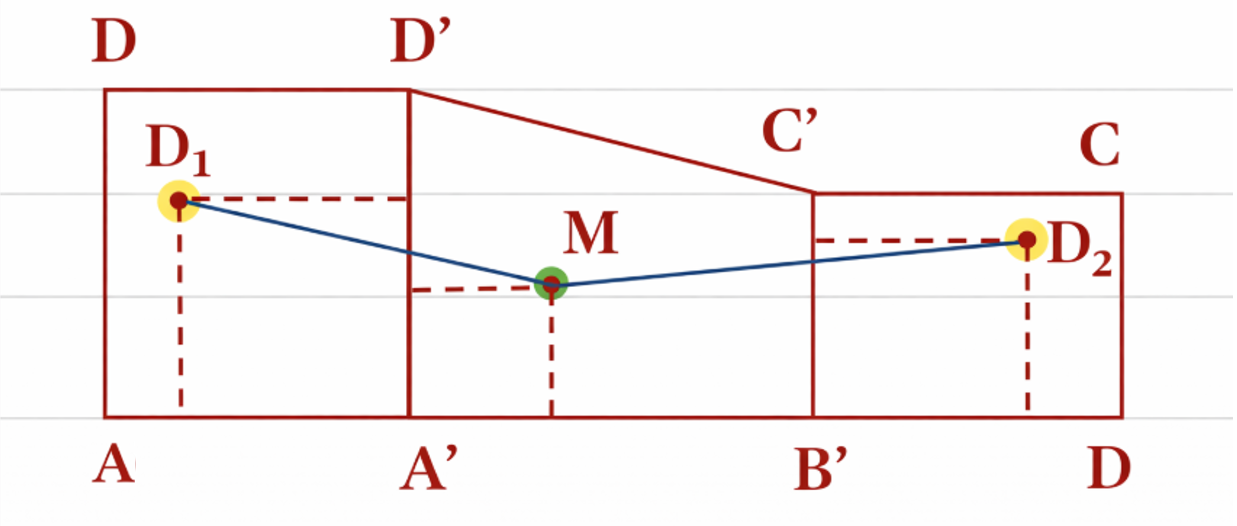
Theo các thông số đề bài cho ta có thể mô hình hóa bài toán bằng hình vẽ sau
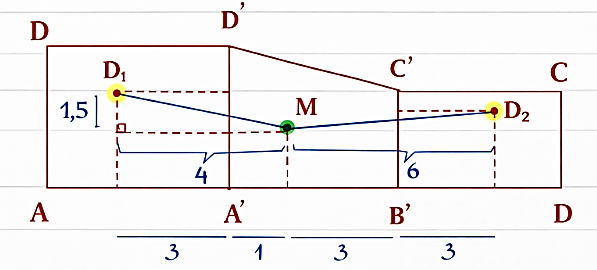
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.