khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Vào học
Đăng nhập
Tạo VIP
Xin chào! Vào học
  2. Phòng luyện thi ĐGNL - ĐGTD
  3. ĐHSP Hà Nội

Câu hỏi:

23/01/2026 2,518 Lưu

Phần I (4 điểm). Thí sinh trả lời từ câu 1 đến câu 16. Đối với mỗi câu, thí sinh chỉ chọn một phương án. Đối với mỗi câu trả lời đúng, thí sinh được 0,25 điểm.

Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x - 2} \right)\left( {x + 1} \right),\forall x \in \mathbb{R}\). Mệnh đề nào dưới đây đúng?    

A. Hàm số đã cho đồng biến trên \(\left( { - 1; + \infty } \right)\).                  
B. Hàm số đã cho đồng biến trên \(\left( { - \infty ;2} \right)\).    
C. Hàm số đã cho nghịch biến trên \(\left( { - 2;1} \right)\).                     
D. Hàm số đã cho nghịch biến trên \[\left( { - 1;2} \right)\].
Xem lời giải

Câu hỏi trong đề: Đề thi tham khảo ĐGNL ĐHSP Hà Nội (SPT) môn Toán 2026 !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Ta có \(f'\left( x \right) = \left( {x - 2} \right)\left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 1\end{array} \right..\)

Bảng xét dấu của \(f'\left( x \right)\) như sau:

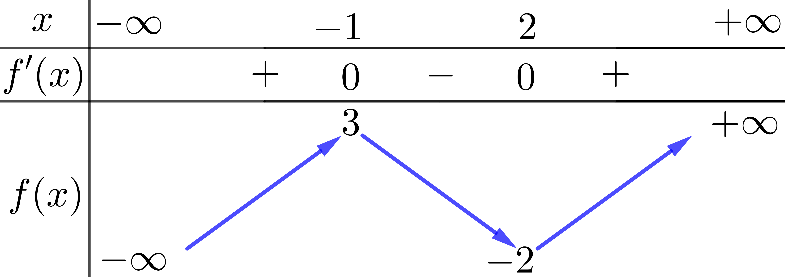
Cho hàm số \(y = f\left( x \right)\) có đạo (ảnh 1)

Vậy hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right),\left( {2; + \infty } \right)\) và nghịch biến trên khoảng \[\left( { - 1;2} \right)\].

Chọn D.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong một kì thi tốt nghiệp trung học phổ thông, một tỉnh X có 80% học sinh lựa chọn tổ hợp A00 (gồm các môn Toán, Vật lí, Hoá học). Biết rằng, nếu một học sinh chọn tổ hợp A00 thì xác suất để học sinh đó đỗ đại học là 0,6; còn nếu một học sinh không chọn tổ hợp A00 thì xác suất để học sinh đó đỗ đại học là 0,7. Chọn ngẫu nhiên một học sinh của tỉnh X đã tốt nghiệp trung học phổ thông trong kì thi trên. Biết rằng học sinh này đã đỗ đại học, tính xác suất để học sinh đó chọn tổ hợp A00.

______

Lời giải

Đáp án:

1. 24/31

Gọi biến cố A: “Học sinh đó chọn tổ hợp A00” ;

biến cố B: “Học sinh đó đỗ đại học”.

Ta cần tính \[P\left( {A|B} \right)\].

Theo bài ra ta có: \(P\left( A \right) = 0,8;P\left( {\overline A } \right) = 1 - P\left( A \right) = 1 - 0,8 = 0,2\).

Ta có \(P\left( {B|A} \right)\) là xác suất để một học sinh đỗ đại học với điều kiện học sinh đó chọn tổ hợp A00 nên \(P\left( {B|A} \right) = 0,6\) và \(P\left( {B|\overline A } \right)\) là xác suất để một học sinh đỗ đại học với điều kiện học sinh đó không chọn tổ hợp A00 nên \(P\left( {B|\overline A } \right) = 0,7\).

Áp dụng công thức Bayes ta được

\(P\left( {A|B} \right) = \frac{{P\left( A \right) \cdot P\left( {B|A} \right)}}{{P\left( A \right) \cdot P\left( {B|A} \right) + P\left( {\overline A } \right) \cdot P\left( {B|\overline A } \right)}} = \frac{{0,8 \cdot 0,6}}{{0,8 \cdot 0,6 + 0,2 \cdot 0,7}} = \frac{{24}}{{31}}\).

Trả lời: \(\frac{{24}}{{31}}\).

Câu 2

(1 điểm). Một cái bình cổ có hình dạng như Hình a. Giả sử mô hình toán mô phỏng việc tạo thành cái bình cổ đó bằng cách xoay phần diện tích (gạch sọc) được giới hạn bởi đường cong \(f\left( x \right) = {x^2} - 8x + 12\) và \(g\left( x \right) = - x + 6\) quanh trục \(Ox\) như Hình b. Hãy tính thể tích của cái bình cổ đó.

Một cái bình cổ có hình dạng như Hình a. Giả sử mô hình toán mô phỏng việc tạo thành cái bình cổ đó bằng cách xoay phần diện tích (gạch sọc) được giới hạn bởi đường cong (ảnh 1)

Lời giải

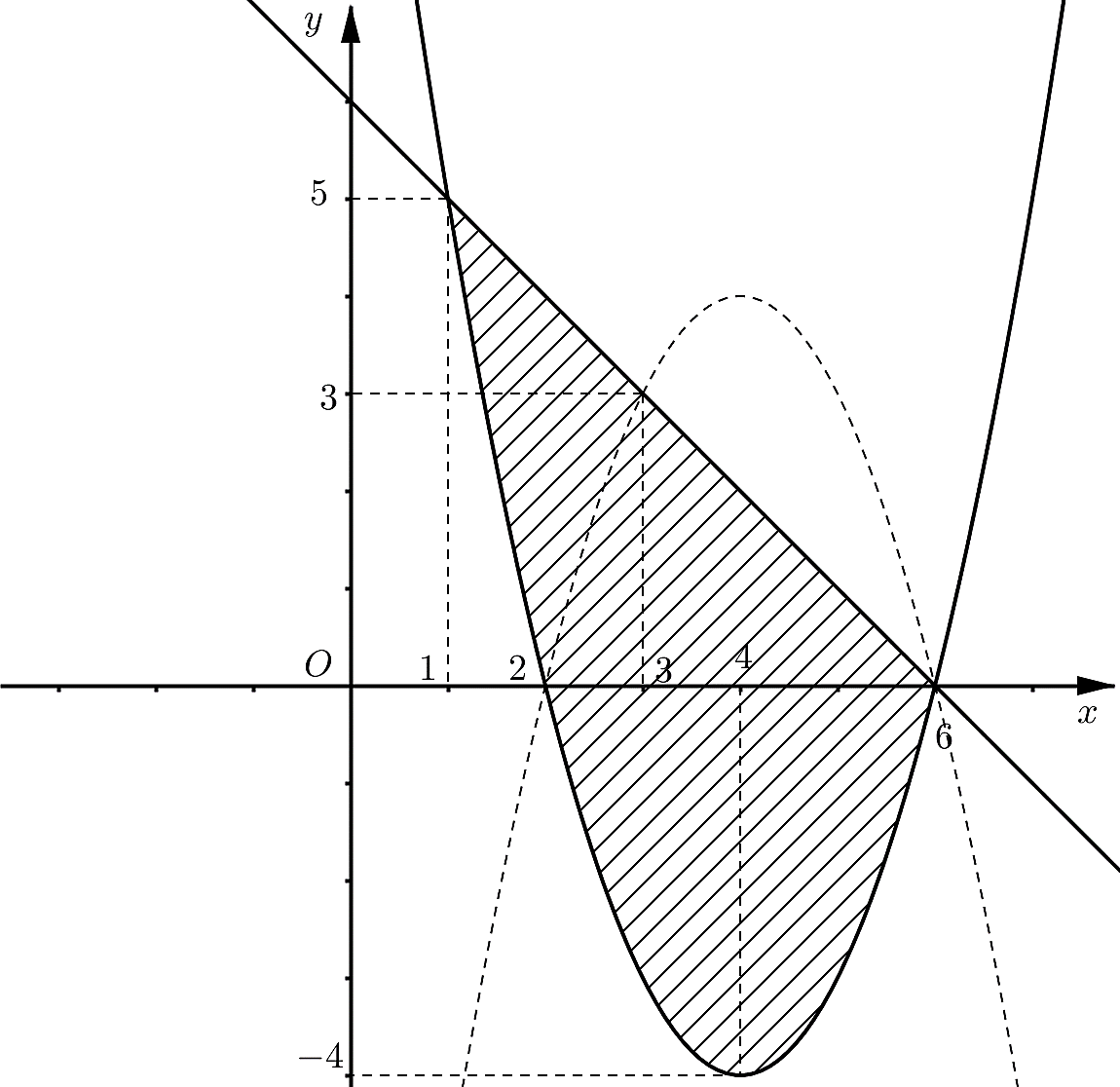
Một cái bình cổ có hình dạng như Hình a. Giả sử mô hình toán mô phỏng việc tạo thành cái bình cổ đó bằng cách xoay phần diện tích (gạch sọc) được giới hạn bởi đường cong (ảnh 2)

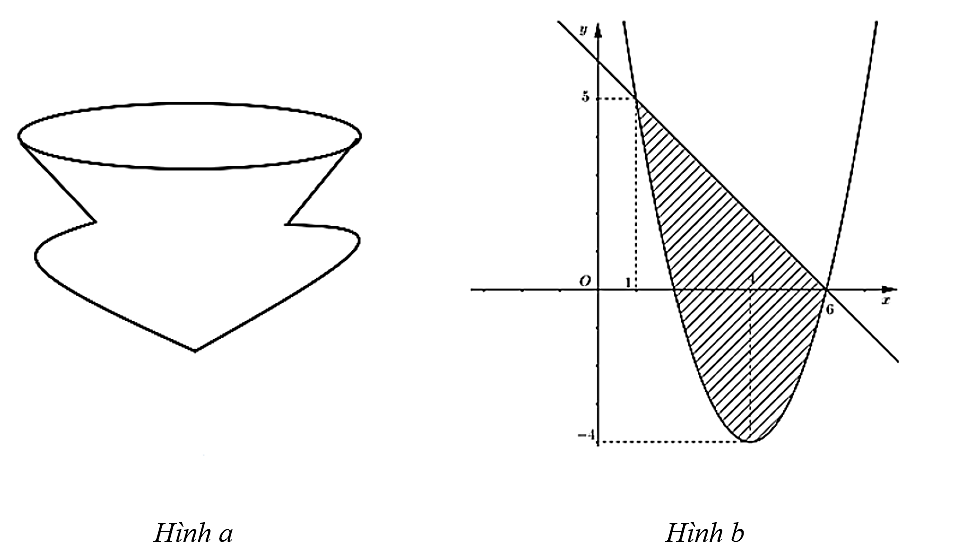
Xét đồ thị hàm số \(y = h\left( x \right) = - f\left( x \right)\) có đồ thị là đường nét đứt đoạn như hình vẽ trên.

Hoành độ giao điểm của đồ thị hàm số \(g\left( x \right)\) và \(h\left( x \right)\) là nghiệm của phương trình \[ - {x^2} + 8x - 12 = - x + 6\] \[ \Leftrightarrow {x^2} - 9x + 18 = 0 \Leftrightarrow x = 3\] hoặc \[x = 6\].

Thể tích của bình cổ là

\(V = \pi \int\limits_3^6 {\left[ {{{\left( { - {x^2} + 8x - 12} \right)}^2}} \right]{\rm{d}}x + \pi \int\limits_1^3 {{{\left( { - x + 6} \right)}^2}{\rm{d}}x - \pi \int\limits_1^2 {{{\left( {{x^2} - 8x + 12} \right)}^2}{\rm{d}}x} } } \)\( = \frac{{153}}{5}\pi + \frac{{98}}{3}\pi - \frac{{113}}{{15}}\pi = \frac{{836}}{{15}}\pi \).

Câu 3

Một hộp đựng 8 thẻ được đánh số từ 2 đến 9. Bạn Lê lấy ngẫu nhiên một thẻ, ghi lại số trên thẻ rồi bỏ thẻ vào hộp. Lần thứ hai, bạn Lê cũng lấy ngẫu nhiên một thẻ, ghi lại số trên thẻ rồi bỏ thẻ vào hộp. Tiếp tục như vậy, sau năm lần bạn Lê đã ghi lại được 5 số. Tính xác suất để trong 5 số ghi được có đúng 2 số chia hết cho 4.

________

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Phần IV (3 điểm). Thí sinh trả lời từ câu 5 đến câu 7. Đối với mỗi câu, thí sinh viết quá trình và kết quả suy luận.

(1 điểm). Giải phương trình: \[{4^{{x^2} - 3x + 2}} + {4^{2{x^2} + 6x + 5}} = {4^{3{x^2} + 3x + 7}} + 1\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

(1 điểm). Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác vuông tại \(A\), \(AB = a,AC = a\sqrt 3 \). Gọi \(M\) là trung điểm của \(CC'\). Biết góc giữa mặt phẳng \(\left( {A'B'M} \right)\) và mặt phẳng đáy bằng \(30^\circ \). Tính khoảng cách giữa hai đường thẳng \(AB\) và \(B'M\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Phần III (1 điểm). Thí sinh trả lời từ câu 1 đến câu 4. Đối với mỗi câu, thí sinh chỉ viết kết quả, không trình bày suy luận. Đối với mỗi câu trả lời đúng, thí sinh được 0,25 điểm.

Giả sử doanh số của một sản phẩm mới tuân theo quy luật logistic được mô hình hóa bằng hàm số \(f\left( t \right) = \frac{{5\,000}}{{1 + 5{{\rm{e}}^{ - t}}}},\,t \ge 0\), trong đó thời gian \[t\] được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm \[f'\left( t \right)\] sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?

____

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack87. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập