Một người săn thỏ trong rừng, khả năng anh ta bắn trúng thỏ trong mỗi lần bắt tỷ lệ nghịch với khoảng cách bắn. Anh ta bắn lần đầu ở khoảng cách \(20\,{\rm{m}}\) với xác suất trúng thỏ là \(0,5\); nếu bị trượt anh ta bắn viên thứ \(2\) ở khoảng cách \(30\,{\rm{m}}\), nếu lại trượt anh ta bắn viên thứ \(3\) ở khoảng cách \(50\,{\rm{m}}.\) Tính xác suất để người thợ săn bắn trúng thỏ sau nhiều nhất ba lần bắt.

______

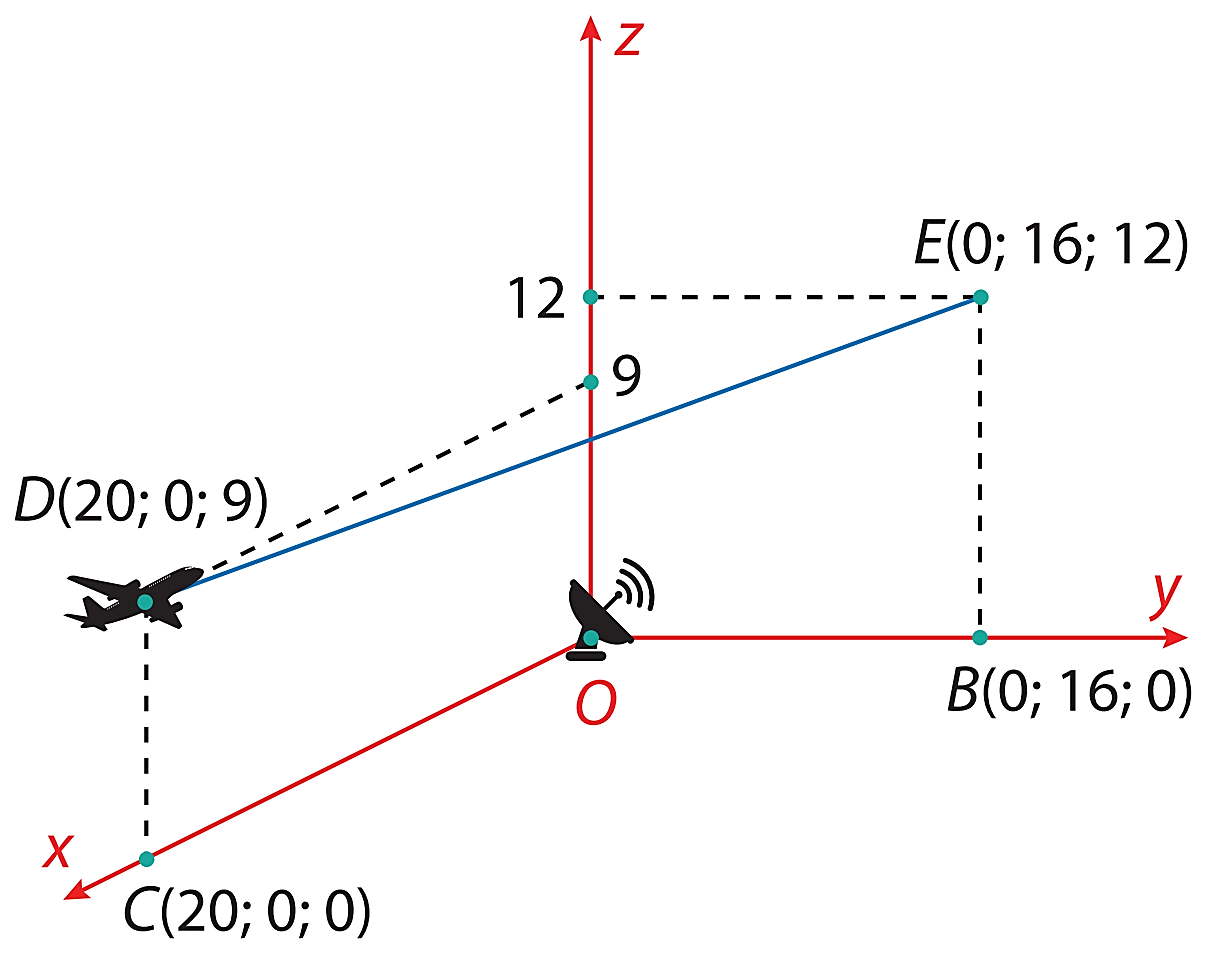
a) Sai. Ta có \(\overrightarrow {OD} = \left( {20\,;0\,;9} \right)\) và \(OD = \sqrt {{{20}^2} + {9^2}} = \sqrt {481} \)km \( \approx 22000\) m.

b) Đúng. Tọa độ trung điểm \(I\) của \(DE\) là \(\left( {10;8;\frac{{21}}{2}} \right).\)

Khi máy bay bay đến điểm \(I,\) máy bay cách mặt đất \(\frac{{21}}{2}\)km hay \(10500\)m.

c) Đúng. Ta có \(\overrightarrow {DE} = \left( { - 20;16;3} \right)\).

Đường thẳng \(DE\) đi qua điểm \(D\left( {20;0;9} \right)\) và có vectơ chỉ phương \(\vec u = \overrightarrow {DE} = \left( { - 20\,;16\,;3} \right)\) nên có phương trình tham số là \(\left\{ \begin{array}{l}x = 20 - 20t\\y = 16t\\z = 9 + 3t\end{array} \right.,(t \in \mathbb{R}).\)

Thay tọa độ điểm \(P\left( {16;3,2;9,6} \right)\) vào phương trình tham số của đường thẳng \(DE\) ta được

\(\left\{ \begin{array}{l}16 = 20 - 20t\\3,2 = 16t\\9,6 = 9 + 3t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 0,2\\t = 0,2\\t = 0,2\end{array} \right.\). Như vậy \(P \in DE.\)

Do đó trên đoạn đường bay từ \(D\) đến \(E,\) máy bay sẽ đi qua điểm \(P\left( {16;3,2;9,6} \right)\).

d) Sai. Gọi \(H\left( {20 - 20t;16t;9 + 3t} \right) \in DE\) là hình chiếu của \(O\) trên \(DE.\)

Hai vectơ \(\left\{ \begin{array}{l}\overrightarrow {OH} = \left( {20 - 20t;16t;9 + 3t} \right)\\\overrightarrow {DE} = \left( { - 20;16;3} \right)\end{array} \right.\) vuông góc với nhau nên

\(\overrightarrow {OH} \cdot \overrightarrow {DE} = 0 \Leftrightarrow - 20\left( {20 - 20t} \right) + 16 \cdot 16t + 3\left( {9 + 3t} \right) = 0 \Leftrightarrow t = \frac{{373}}{{665}}.\)

Khi đó \(\overrightarrow {OH} = \left( {\frac{{1168}}{{133}};\frac{{5968}}{{665}};\frac{{7104}}{{665}}} \right)\) và \(OH = \sqrt {{{\left( {\frac{{1168}}{{133}}} \right)}^2} + {{\left( {\frac{{5968}}{{665}}} \right)}^2} + {{\left( {\frac{{7104}}{{665}}} \right)}^2}} = \sqrt {\frac{{180736}}{{665}}} = \frac{{16\sqrt {469490} }}{{665}}.\)

Khoảng cách giữa vị trí đầu tiên và vị trí cuối cùng mà máy bay bay trong phạm vi theo dõi của ra đa là:

\(2\sqrt {{{20}^2} - O{H^2}} = 2\sqrt {{{20}^2} - \frac{{180736}}{{665}}} = \frac{{584\sqrt {665} }}{{665}} \approx 22600\) m.

Cách 1.

Thể tích khối tứ diện \(A.A\prime BD\) (hoặc \(A\prime .ABD\)) là: \(V = \frac{1}{3} \cdot {S_{\Delta A\prime BD}} \cdot d\left( {A,\left( {A\prime BD} \right)} \right) = \frac{1}{3} \cdot {S_{\Delta ABD}} \cdot d\left( {A\prime ,\left( {ABD} \right)} \right)\).

Ta có \(d\left( {A\prime ,\left( {ABD} \right)} \right) = AA' = 6\) và \({S_{\Delta ABD}} = \frac{1}{2} \cdot AB \cdot AD = \frac{1}{2} \cdot 6 \cdot 6 = 18\).

Thể tích khối tứ diện \(A.A\prime BD\) (hoặc \(A\prime .ABD\)): \(V = \frac{1}{3} \cdot {S_{\Delta ABD}} \cdot AA\prime = \frac{1}{3} \cdot 18 \cdot 6 = 36\).

Tam giác \(A\prime BD\) là tam giác đều cạnh \(6\sqrt 2 \) nên \({S_{\Delta A\prime BD}} = \frac{{{{\left( {6\sqrt 2 } \right)}^2} \cdot \sqrt 3 }}{4} = \frac{{36 \cdot 2 \cdot \sqrt 3 }}{4} = \frac{{72\sqrt 3 }}{4} = 18\sqrt 3 \).

Khi đó, \(V = \frac{1}{3} \cdot {S_{\Delta A\prime BD}} \cdot d\left( {A,\left( {A\prime BD} \right)} \right)\)\( \Leftrightarrow 36 = \frac{1}{3} \cdot \left( {18\sqrt 3 } \right) \cdot d\left( {A,\left( {A\prime BD} \right)} \right)\)

\( \Leftrightarrow 36 = 6\sqrt 3 \cdot d\left( {A,\left( {A\prime BD} \right)} \right)\)\( \Leftrightarrow d\left( {A,\left( {A\prime BD} \right)} \right) = \frac{{36}}{{6\sqrt 3 }} = \frac{6}{{\sqrt 3 }} = \frac{{6\sqrt 3 }}{3} = 2\sqrt 3 \).

Cách 2.

Gọi \(O = AC \cap BD\), ta có \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot AA'\end{array} \right. \Rightarrow BD \bot \left( {AA'O} \right) \Rightarrow \left( {AA'O} \right) \bot \left( {A'BD} \right)\) theo giao tuyến \(A'O\).

Dựng \(AH \bot A'O \Rightarrow AH \bot \left( {A'BD} \right) \Rightarrow d\left( {A,\left( {A'BD} \right)} \right) = AH\).

\(\Delta A'AO\) vuông tại \(A\) có \(A'A = 6\); \(AO = \frac{{AC}}{2} = 3\sqrt 2 \).

\( \Rightarrow AH = \frac{{AA' \cdot AO}}{{A'O}} = \frac{{AA' \cdot AO}}{{\sqrt {A'{O^2} + A{O^2}} }} = \frac{{6 \cdot 3\sqrt 2 }}{{\sqrt {36 + 18} }} = 2\sqrt 3 \). Vậy \(d\left( {A,\left( {A\prime BD} \right)} \right) = AH = 2\sqrt 3 \).