(1 điểm). Cho hình lập phương \(ABCD.A\prime B\prime C\prime D\prime \) có cạnh bằng 6. Tính khoảng cách từ điểm \(A\) tới mặt phẳng \(\left( {A\prime BD} \right)\).
(1 điểm). Cho hình lập phương \(ABCD.A\prime B\prime C\prime D\prime \) có cạnh bằng 6. Tính khoảng cách từ điểm \(A\) tới mặt phẳng \(\left( {A\prime BD} \right)\).
Câu hỏi trong đề: Đề ôn thi ĐGNL ĐHSP Hà Nội môn Toán có đáp án !!
Quảng cáo
Trả lời:
Cách 1.
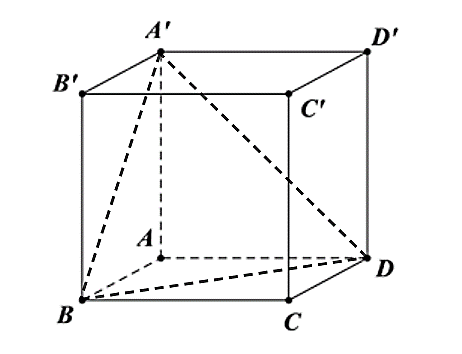
Thể tích khối tứ diện \(A.A\prime BD\) (hoặc \(A\prime .ABD\)) là: \(V = \frac{1}{3} \cdot {S_{\Delta A\prime BD}} \cdot d\left( {A,\left( {A\prime BD} \right)} \right) = \frac{1}{3} \cdot {S_{\Delta ABD}} \cdot d\left( {A\prime ,\left( {ABD} \right)} \right)\).
Ta có \(d\left( {A\prime ,\left( {ABD} \right)} \right) = AA' = 6\) và \({S_{\Delta ABD}} = \frac{1}{2} \cdot AB \cdot AD = \frac{1}{2} \cdot 6 \cdot 6 = 18\).
Thể tích khối tứ diện \(A.A\prime BD\) (hoặc \(A\prime .ABD\)): \(V = \frac{1}{3} \cdot {S_{\Delta ABD}} \cdot AA\prime = \frac{1}{3} \cdot 18 \cdot 6 = 36\).
Tam giác \(A\prime BD\) là tam giác đều cạnh \(6\sqrt 2 \) nên \({S_{\Delta A\prime BD}} = \frac{{{{\left( {6\sqrt 2 } \right)}^2} \cdot \sqrt 3 }}{4} = \frac{{36 \cdot 2 \cdot \sqrt 3 }}{4} = \frac{{72\sqrt 3 }}{4} = 18\sqrt 3 \).
Khi đó, \(V = \frac{1}{3} \cdot {S_{\Delta A\prime BD}} \cdot d\left( {A,\left( {A\prime BD} \right)} \right)\)\( \Leftrightarrow 36 = \frac{1}{3} \cdot \left( {18\sqrt 3 } \right) \cdot d\left( {A,\left( {A\prime BD} \right)} \right)\)
\( \Leftrightarrow 36 = 6\sqrt 3 \cdot d\left( {A,\left( {A\prime BD} \right)} \right)\)\( \Leftrightarrow d\left( {A,\left( {A\prime BD} \right)} \right) = \frac{{36}}{{6\sqrt 3 }} = \frac{6}{{\sqrt 3 }} = \frac{{6\sqrt 3 }}{3} = 2\sqrt 3 \).
Cách 2.
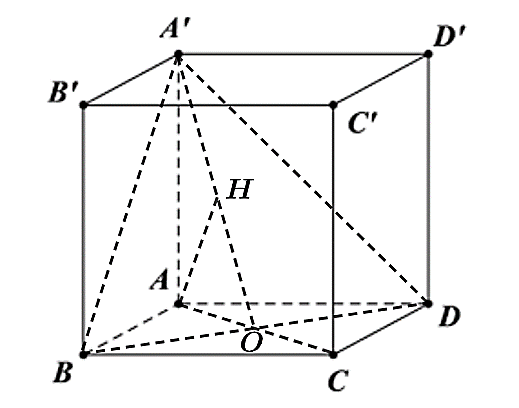
Gọi \(O = AC \cap BD\), ta có \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot AA'\end{array} \right. \Rightarrow BD \bot \left( {AA'O} \right) \Rightarrow \left( {AA'O} \right) \bot \left( {A'BD} \right)\) theo giao tuyến \(A'O\).
Dựng \(AH \bot A'O \Rightarrow AH \bot \left( {A'BD} \right) \Rightarrow d\left( {A,\left( {A'BD} \right)} \right) = AH\).
\(\Delta A'AO\) vuông tại \(A\) có \(A'A = 6\); \(AO = \frac{{AC}}{2} = 3\sqrt 2 \).
\( \Rightarrow AH = \frac{{AA' \cdot AO}}{{A'O}} = \frac{{AA' \cdot AO}}{{\sqrt {A'{O^2} + A{O^2}} }} = \frac{{6 \cdot 3\sqrt 2 }}{{\sqrt {36 + 18} }} = 2\sqrt 3 \). Vậy \(d\left( {A,\left( {A\prime BD} \right)} \right) = AH = 2\sqrt 3 \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
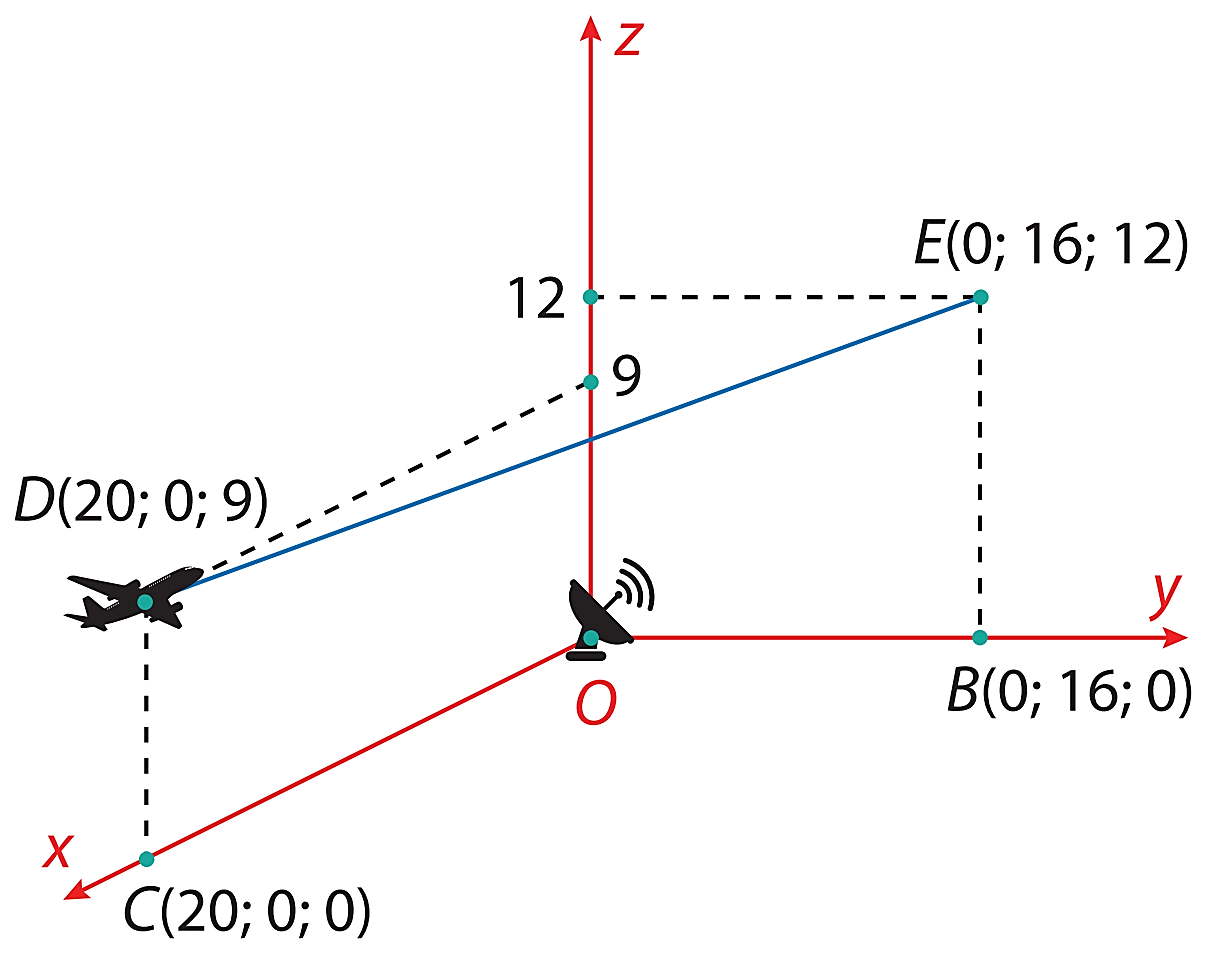
a) Sai. Ta có \(\overrightarrow {OD} = \left( {20\,;0\,;9} \right)\) và \(OD = \sqrt {{{20}^2} + {9^2}} = \sqrt {481} \)km \( \approx 22000\) m.
b) Đúng. Tọa độ trung điểm \(I\) của \(DE\) là \(\left( {10;8;\frac{{21}}{2}} \right).\)
Khi máy bay bay đến điểm \(I,\) máy bay cách mặt đất \(\frac{{21}}{2}\)km hay \(10500\)m.
c) Đúng. Ta có \(\overrightarrow {DE} = \left( { - 20;16;3} \right)\).
Đường thẳng \(DE\) đi qua điểm \(D\left( {20;0;9} \right)\) và có vectơ chỉ phương \(\vec u = \overrightarrow {DE} = \left( { - 20\,;16\,;3} \right)\) nên có phương trình tham số là \(\left\{ \begin{array}{l}x = 20 - 20t\\y = 16t\\z = 9 + 3t\end{array} \right.,(t \in \mathbb{R}).\)
Thay tọa độ điểm \(P\left( {16;3,2;9,6} \right)\) vào phương trình tham số của đường thẳng \(DE\) ta được
\(\left\{ \begin{array}{l}16 = 20 - 20t\\3,2 = 16t\\9,6 = 9 + 3t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 0,2\\t = 0,2\\t = 0,2\end{array} \right.\). Như vậy \(P \in DE.\)
Do đó trên đoạn đường bay từ \(D\) đến \(E,\) máy bay sẽ đi qua điểm \(P\left( {16;3,2;9,6} \right)\).
d) Sai. Gọi \(H\left( {20 - 20t;16t;9 + 3t} \right) \in DE\) là hình chiếu của \(O\) trên \(DE.\)
Hai vectơ \(\left\{ \begin{array}{l}\overrightarrow {OH} = \left( {20 - 20t;16t;9 + 3t} \right)\\\overrightarrow {DE} = \left( { - 20;16;3} \right)\end{array} \right.\) vuông góc với nhau nên
\(\overrightarrow {OH} \cdot \overrightarrow {DE} = 0 \Leftrightarrow - 20\left( {20 - 20t} \right) + 16 \cdot 16t + 3\left( {9 + 3t} \right) = 0 \Leftrightarrow t = \frac{{373}}{{665}}.\)
Khi đó \(\overrightarrow {OH} = \left( {\frac{{1168}}{{133}};\frac{{5968}}{{665}};\frac{{7104}}{{665}}} \right)\) và \(OH = \sqrt {{{\left( {\frac{{1168}}{{133}}} \right)}^2} + {{\left( {\frac{{5968}}{{665}}} \right)}^2} + {{\left( {\frac{{7104}}{{665}}} \right)}^2}} = \sqrt {\frac{{180736}}{{665}}} = \frac{{16\sqrt {469490} }}{{665}}.\)
Khoảng cách giữa vị trí đầu tiên và vị trí cuối cùng mà máy bay bay trong phạm vi theo dõi của ra đa là:
\(2\sqrt {{{20}^2} - O{H^2}} = 2\sqrt {{{20}^2} - \frac{{180736}}{{665}}} = \frac{{584\sqrt {665} }}{{665}} \approx 22600\) m.
Lời giải
Gọi \({A_k}\) là biến cố: “Người thợ săn bắn trúng thỏ ở lần thứ \(k\)”; \(k = 1,2,3.\)
Theo đầu bài ta có: \(P\left( {{A_1}} \right) = 0,5\); \(P\left( {{A_2}|\overline {{A_1}} } \right) = \frac{{20 \times 0,5}}{{30}} = \frac{1}{3}\); \(P\left( {{A_3}|\overline {{A_1}} \,\overline {{A_2}} } \right) = \frac{{20 \times 0,5}}{{50}} = \frac{1}{5}.\)
Gọi \(A\) là biến cố: “Người thợ săn bắn trúng thỏ”. Khi đó: \(A = {A_1} \cup \overline {{A_1}} {A_2} \cup \overline {{A_1}} \,\overline {{A_2}} {A_3}.\)
Vì \(3\) biến cố \({A_1}\), \(\overline {{A_1}} {A_2}\), \(\overline {{A_1}} \,\overline {{A_2}} {A_3}\) xung khắc từng đôi nên: \(P\left( A \right) = P\left( {{A_1}} \right) + P\left( {\overline {{A_1}} {A_2}} \right) + P\left( {\overline {{A_1}} \overline {{A_2}} {A_3}} \right).\)
Theo công thức nhân xác suất \(P\left( {\overline {{A_1}} {A_2}} \right) = P\left( {\overline {{A_1}} } \right) \cdot P\left( {{A_2}|\overline {{A_1}} } \right) = \left[ {1 - P\left( {{A_1}} \right)} \right] \cdot P\left( {{A_2}|\overline {{A_1}} } \right)\)\( = \left( {1 - 0,5} \right) \times \frac{1}{3} = \frac{1}{6}.\)
Tương tự \(P\left( {\overline {{A_1}} \,\overline {{A_2}} {A_3}} \right) = P\left( {\overline {{A_1}} } \right) \cdot P\left( {\overline {{A_2}} |\overline {{A_1}} } \right) \cdot P\left( {{A_3}|\overline {{A_1}} \,\overline {{A_2}} } \right)\)
\( = \left[ {1 - P\left( {{A_1}} \right)} \right] \cdot P\left[ {1 - P\left( {{A_2}|\overline {{A_1}} } \right)} \right] \cdot P\left( {{A_3}|\overline {{A_1}} \,\overline {{A_2}} } \right) = \left( {1 - 0,5} \right)\left( {1 - \frac{1}{3}} \right) \times \frac{1}{5} = \frac{1}{{15}}.\)
Do đó: \(P\left( A \right) = 0,5 + \frac{1}{6} + \frac{1}{{15}} = \frac{{11}}{{15}}.\)
Trả lời: \(\frac{{11}}{{15}}\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.