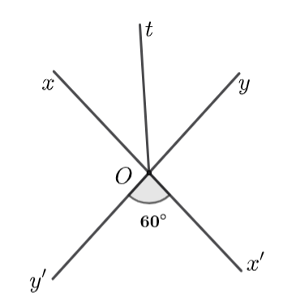
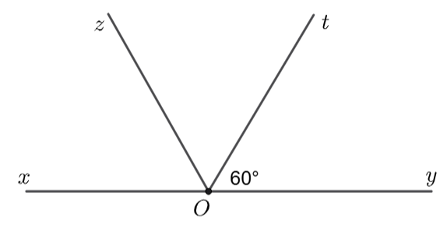
Cho điểm \(O\) thuộc đường thẳng \(xy.\) Vẽ các tia \(Oz,\,\,Ot\) về cùng một phía sao cho \(\widehat {yOt} = 60^\circ ,\) \(\widehat {yOz} = 120^\circ \).
Khi đó,
Cho điểm \(O\) thuộc đường thẳng \(xy.\) Vẽ các tia \(Oz,\,\,Ot\) về cùng một phía sao cho \(\widehat {yOt} = 60^\circ ,\) \(\widehat {yOz} = 120^\circ \).

Khi đó,
a) \(\widehat {tOz} = 60^\circ \).
b) \(Ot\) là phân giác của \(\widehat {yOz}.\)
c) \(\widehat {xOz} < 60^\circ \).
Quảng cáo
Trả lời:
a) Đúng.
Nhận thấy \(\widehat {yOt}\) và \(\widehat {tOz}\) là hai góc kề nhau nên \(\widehat {tOz} + \widehat {yOt} = \widehat {yOz}\).
Do đó, \(\widehat {tOz} = \widehat {yOz} - \widehat {yOt} = 120^\circ - 60^\circ = 60^\circ \).
b) Đúng.
Vì \(\widehat {tOz} = \widehat {yOt} = 60^\circ \) và tia \(Ot\) nằm giữa hai tia \(Oy,\,\,Oz\).
Do đó, \(Ot\) là phân giác của \(\widehat {yOz}.\)
c) Sai.
Có \(\widehat {xOz},\,\,\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOz} + \widehat {yOz} = 180^\circ \) hay \(\widehat {xOz} = 180^\circ - \widehat {yOz} = 180^\circ - 120^\circ = 60^\circ \).
d) Đúng.
Vì \(\widehat {tOz} = \widehat {zOx} = 60^\circ \) và \(Oz\) nằm giữa hai tia \(Ox,\,\,Oz\).
Do đó, \(Oz\) là tia phân giác của \(\widehat {xOt}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
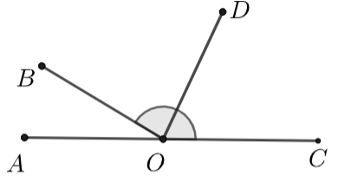
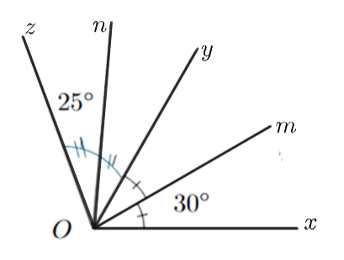
Câu 1
a) \(\widehat {BOA} = 36^\circ .\)
b) \(\widehat {BOC} = 150^\circ .\)
c) \(\widehat {DOC} = 75^\circ .\)
Lời giải
a) Sai.
Ta có: \(\widehat {AOB}\) và \(\widehat {BOC}\) là hai góc kề bù nên \(\widehat {COB} + \widehat {AOB} = 180^\circ \) hay \(5\widehat {AOB} + \widehat {AOB} = 180^\circ \).
Suy ra \(6\widehat {AOB} = 180^\circ \).
Do đó \(\widehat {AOB} = 180^\circ :6 = 30^\circ \).
b) Đúng.
Có \(\widehat {BOC} = 5\widehat {AOB} = 5 \cdot 30^\circ = 150^\circ .\)
c) Đúng.
Có \(OD\) là tia phân giác của \(\widehat {BOC}\) nên \(\widehat {DOC} = \widehat {BOD} = \widehat {\frac{{BOC}}{2}} = \frac{{150^\circ }}{2} = 75^\circ .\)
d) Sai.
Có \(\widehat {DOA} = \widehat {AOB} + \widehat {BOD} = 30^\circ + 75^\circ = 105^\circ \).
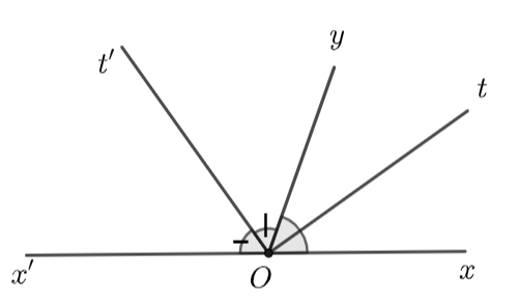
Câu 2
a) \(\widehat {x'Oy} = 110^\circ .\)
b) \(\widehat {xOt} = 45^\circ .\)
c) \(\widehat {tOt'} = 90^\circ .\)
Lời giải
a) Đúng.
Vì \[\widehat {xOy}\] và \(\widehat {x'Oy}\) là hai góc kề bù nên ta có \(\widehat {xOy} + \widehat {yOx'} = 180^\circ \).
Suy ra \(\widehat {yOx'} = 180^\circ - \widehat {xOy} = 180^\circ - 70^\circ = 110^\circ \).
b) Sai.
Có \(Ot\) là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {tOy} = \widehat {tOx} = \frac{{70^\circ }}{2} = 35^\circ \).
c) Đúng.
Vì \(Ot'\) là tia phân giác của \(\widehat {x'Oy}\) nên \(\widehat {t'Oy} = \widehat {t'Ox'} = \frac{{110^\circ }}{2} = 55^\circ \).
Do đó, \(\widehat {tOt'} = \widehat {tOy} + \widehat {t'Oy} = 55^\circ + 35^\circ = 90^\circ .\)
d) Đúng.
Có \(\widehat {xOt'} = \widehat {xOy} + \widehat {t'Oy} = 70^\circ + 55^\circ = 125^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
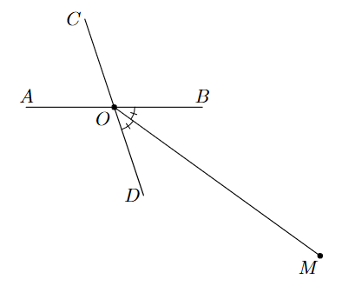
Câu 4
A. \(\widehat {xOy} = \widehat {yOt.}\)
B. \(\widehat {xOt} + \widehat {yOt} = \widehat {xOy}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.