Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc \(v\left( t \right) = 7t\,\,(\;{\rm{m}}/{\rm{s}})\), đi được 5 giây thì người lái xe phát hiện chướng ngại vật và phanh gấp. Ô tô tiếp tục chuyển động chậm dần đều với gia tốc \(a = - 70\,\,\left( {{\rm{m}}/{{\rm{s}}^2}} \right).\) Quãng đường đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn là:
Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc \(v\left( t \right) = 7t\,\,(\;{\rm{m}}/{\rm{s}})\), đi được 5 giây thì người lái xe phát hiện chướng ngại vật và phanh gấp. Ô tô tiếp tục chuyển động chậm dần đều với gia tốc \(a = - 70\,\,\left( {{\rm{m}}/{{\rm{s}}^2}} \right).\) Quãng đường đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn là:
Câu hỏi trong đề: Đề tham khảo ĐGNL ĐHQG Hà Nội (HSA) năm 2026-2027 (Đề 14) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vận tốc ô tô tại thời điểm bắt đầu phanh là \({v_1}\left( 5 \right) = 35\,\,(\;{\rm{m}}/{\rm{s}}).\)
Vận tốc của chuyển động sau khi phanh là \({v_2}\left( t \right) = - 70t + c.\)
Do \({v_2}\left( 0 \right) = 35\,\,(\;{\rm{m}}/{\rm{s}}) \Rightarrow c = 35 \Rightarrow {v_2}\left( t \right) = - 70t + 35.\)
Khi xe dừng hẳn tức là: \({v_2}\left( t \right) = 0 \Rightarrow - 70t + 35 = 0 \Leftrightarrow t = \frac{1}{2}{\rm{. }}\)
Quãng đường \(S\,\,\left( m \right)\) đi được ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn là
\[S\,\,\left( m \right) = \int\limits_0^5 {7t} \,dt + \int\limits_0^{\frac{1}{2}} {\left( { - 70t + 35} \right)} \,dt = 96,25\,\,(\;{\rm{m}})\]. Chọn A.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Gọi biến cố A: “Thỏ được bắt từ chuồng I bỏ sang chuồng II là thỏ trắng”.
Biến cố B: “Thỏ được bắt ra từ chuồng II là thỏ trắng”.
Theo đề ta có: \(P\left( A \right) = \frac{5}{{10}} = \frac{1}{2} \Rightarrow P\left( {\overline A } \right) = \frac{1}{2}\).
Có \(P\left( {B|A} \right) = \frac{7}{{11}};P\left( {B|\overline A } \right) = \frac{6}{{11}}\).
Cần tính: \(P\left( {A|B} \right) = \frac{{P\left( A \right) \cdot P\left( {B|A} \right)}}{{P\left( A \right) \cdot P\left( {B|A} \right) + P\left( {\overline A } \right) \cdot P\left( {B|\overline A } \right)}} = \frac{{\frac{1}{2} \cdot \frac{7}{{11}}}}{{\frac{1}{2} \cdot \frac{7}{{11}} + \frac{1}{2} \cdot \frac{6}{{11}}}} = \frac{7}{{13}}\). Chọn B.
Lời giải
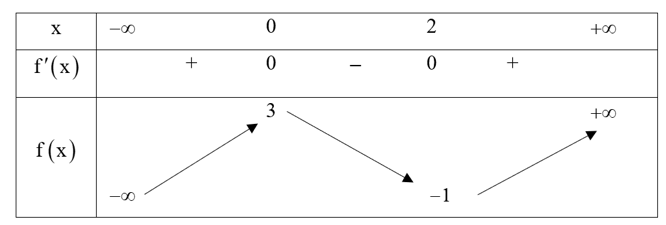
Để đồ thị hàm số \(y = \frac{3}{{f\left( {{x^2}} \right) - m}}\) có 4 đường tiệm cận đứng khi phương trình \(f\left( {{x^2}} \right) = m\) có 4 nghiệm \(x\) phân biệt.
Đặt \(t = {x^2}\,,\,\,t \ge 0.\)
Từ bảng biến thiên của hàm số \(y = f\left( x \right)\) ta thấy, phương trình \(f\left( t \right) = m\) có 2 nghiệm dương \(t\) phân biệt khi \( - 1 < m < 3\).
Với mỗi giá trị \(t > 0\) cho ta 2 giá trị đối nhau của \(x\), nên với điều kiện \( - 1 < m < 3\), phương trình \(f\left( {{x^2}} \right) = m\) có 4 nghiệm \(x\) phân biệt.
Do đó đồ thị hàm số \(y = \frac{3}{{f\left( {{x^2}} \right) - m}}\) có 4 tiệm cận đứng khi \( - 1 < m < 3\).
Vì \(m \in \mathbb{Z}\) nên \(m \in \left\{ {0\,;\,\,1\,;\,\,2} \right\}\).
Đáp án cần nhập là: 3.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập