Một phòng khám đo và ghi lại huyết áp tâm thu (đơn vị tính là \(mmHg\)) của một số người đến khám bệnh thu được kết quả như sau:
118
100
107
135
127
158
179
95
127
130
135
116
182
166
164
99
112
129
134
144
158
97
175
110
99
128
134
192
149
135
90
Theo Hiệp hội Tim mạch Hoa Kỳ, người bình thường có huyết áp tâm thu từ \(90mmHg\) đến dưới \(120mmHg\) , người ở dạng tiền tăng huyết áp có huyết áp tâm thu từ \(120mmHg\) đến dưới \(140mmHg\) ; người bị tăng huyết áp có huyết áp tâm thu lớn hơn hoặc bằng \(140mmHg\) .
Lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm cho dãy số liệu trên theo các mức bệnh huyết áp.
Một phòng khám đo và ghi lại huyết áp tâm thu (đơn vị tính là \(mmHg\)) của một số người đến khám bệnh thu được kết quả như sau:
|
118 |
100 |
107 |
135 |
127 |
158 |
179 |
95 |
127 |
130 |
135 |
116 |
182 |
166 |
164 |
|
|
99 |
112 |
129 |
134 |
144 |
158 |
97 |
175 |
110 |
99 |
128 |
134 |
192 |
149 |
135 |
90 |
Theo Hiệp hội Tim mạch Hoa Kỳ, người bình thường có huyết áp tâm thu từ \(90mmHg\) đến dưới \(120mmHg\) , người ở dạng tiền tăng huyết áp có huyết áp tâm thu từ \(120mmHg\) đến dưới \(140mmHg\) ; người bị tăng huyết áp có huyết áp tâm thu lớn hơn hoặc bằng \(140mmHg\) .
Lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm cho dãy số liệu trên theo các mức bệnh huyết áp.
Quảng cáo
Trả lời:
Bảng tần số ghép nhóm:
|
Mức huyết áp (mmHg) |
\(\left[ {90;120} \right)\) Bình thường |
\(\left[ {120;140} \right)\) Tiền tăng huyết áp |
Từ 140 trở lên Tăng huyết áp |
|
Tần số |
11 |
11 |
9 |
Bảng tần số tương đối ghép nhóm:
|
Mức huyết áp (mmHg) |
\(\left[ {90;120} \right)\) Bình thường |
\(\left[ {120;140} \right)\) Tiền tăng huyết áp |
Từ 140 trở lên Tăng huyết áp |
|
Tần số |
35,5% |
35,5% |
29% |
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Có 8 nhân viên của công ty đi làm hết dưới 15 phút; 15 nhân viên đi làm hết từ 15 phút đến dưới 30 phút; 12 nhân viên đi làm hết từ 30 phút đến dưới 45 phút; 5 nhân viên đi làm hết từ 45 phút đến dưới 60 phút.
Ta có bảng tần số ghép nhóm sau:
|
Thời gian (phút) |
\(\left[ {0;15} \right)\) |
\(\left[ {15;30} \right)\) |
\(\left[ {30;45} \right)\) |
\(\left[ {45;60} \right)\) |
|
Tần số |
8 |
15 |
12 |
5 |
b) Số nhân viên của công ty là \(n = 40\). Các tần số tương đối tương ứng là:
\({f_1} = \frac{8}{{40}}.100\% = 20\% ;{f_2} = \frac{{15}}{{40}}.100\% = 37,5\% \);\({f_3} = \frac{{12}}{{40}}.100\% = 30\% ;{f_4} = \frac{5}{{40}}.100\% = 12,5\% \)
Ta có bảng tần số tương đối ghép nhóm sau:
|
Thời gian (phút) |
\(\left[ {0;15} \right)\) |
\(\left[ {15;30} \right)\) |
\(\left[ {30;45} \right)\) |
\(\left[ {45;60} \right)\) |
|
Tần số tương đối |
\(20{\rm{\% }}\) |
\(37,5{\rm{\% }}\) |
\(30{\rm{\% }}\) |
\(12,5{\rm{\% }}\) |
Lời giải
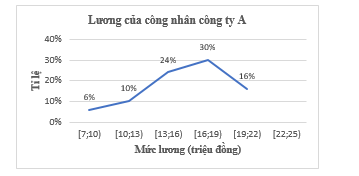
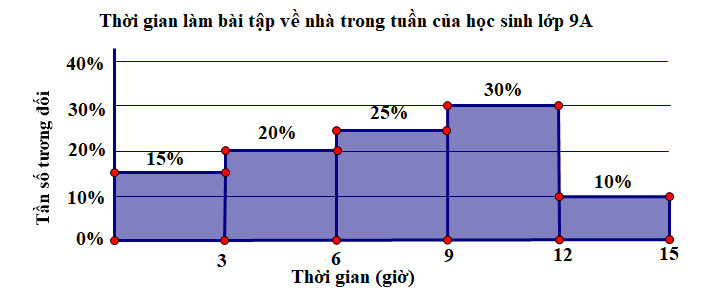
a) Tỉ lệ học sinh trong lớp dành ít nhất 6 giờ trong tuần để làm bài tập về nhà là:\(25\% + 30\% + 10\% = 65\% {\rm{. }}\)
b) Số học sinh lớp 9 A dành ít nhất 6 giờ trong tuần để làm bài tập về nhà là:\(40 \cdot 65\% = 26\) (học sinh).
c) Biểu đồ tần số tương đối ghép nhóm dạng cột:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.