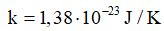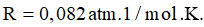Một bong bóng chứa khí Carbon dioxide \(\left( {{\rm{C}}{{\rm{O}}_2}} \right)\) có thể tích \(1\;{\rm{c}}{{\rm{m}}^3}\) được giải phóng bởi một con cá chép bơi ở độ sâu \(2,5\;{\rm{m}}\). Biết khí trong bong bóng là khí lí tưởng và xem nhiệt độ khí không đổi và bằng \({17^\circ }{\rm{C}}\), khối lượng mol của khí Carbon dioxide là \(44\;{\rm{g}}/{\rm{mol}}\). Áp suất khí quyển bằng \({{\rm{P}}_{\rm{o}}}\) \( = {10^5}\;{\rm{Pa}}\), khối lượng riêng của nước là \(\rho = 1000\;{\rm{kg}}/{{\rm{m}}^3}\). Hằng số khí \({\rm{R}} = 8,31\;{\rm{J}}/{\rm{mol}}\). K . Áp suất trong lòng chất lỏng phụ thuộc độ sâu \(h\) theo công thức \(P = {P_o} + \rho gh\). Gia tốc trọng trường \(g = \) \(10\;{\rm{m}}/{{\rm{s}}^2}\).
Quảng cáo
Trả lời:
a) Đúng. \(Dgh = 1000 \cdot 10 \cdot 2,5 = 25 \cdot {10^3}\;{\rm{Pa}} = 25{\rm{kPa}}\)
b) Sai. \(p = {p_0} + Dgh = {10^5} + 25 \cdot {10^3} = 1,25 \cdot {10^5}\;{\rm{Pa}}\)
c) Sai. \(\frac{{pV}}{T} = nR \Rightarrow \frac{{1,25 \cdot {{10}^5} \cdot {{10}^{ - 6}}}}{{17 + 273}} = n \cdot 8,31 \Rightarrow n \approx 5,1869 \cdot {10^{ - 5}}\;{\rm{mol}}\)
\(m = nM = 5,1869 \cdot {10^{ - 5}} \cdot 44 \approx 2,28 \cdot {10^{ - 3}}g = 2,28mg\)
d) Đúng. Đẳng nhiệt \( \Rightarrow {p_0}{V_0} = pV \Rightarrow {10^5}{V_0} = 1,25 \cdot {10^5}.1 \Rightarrow {V_0} = 1,25\;{\rm{c}}{{\rm{m}}^3}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
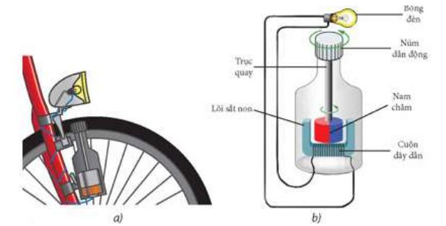
\(r = \frac{d}{2} = \frac{{20}}{2} = 10\;{\rm{mm}}\)
\(\omega = \frac{v}{r} = \frac{{24/3,6}}{{10 \cdot {{10}^{ - 3}}}} = \frac{{2000}}{3}{\rm{rad}}/{\rm{s}}\)
\({E_0} = NBS\omega = 1500 \cdot {10^{ - 2}} \cdot 4 \cdot {10^{ - 4}} \cdot \frac{{2000}}{3} = 4\;{\rm{V}}\)
\(E = \frac{{{E_0}}}{{\sqrt 2 }} = \frac{4}{{\sqrt 2 }} = 2\sqrt 2 V\).Chọn DLời giải
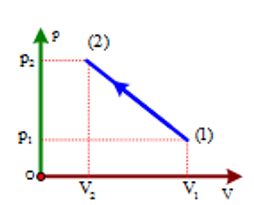
\({p_1}{V_1} = {p_2}{V_2} \Rightarrow {T_1} = {T_2} \Rightarrow {T_{{\rm{max }}}}\) tại trung điểm \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{p = \frac{{{p_1} + {p_2}}}{2} = \frac{{4,5 + 13,5}}{2} = 9\;{\rm{atm}}}\\{V = \frac{{{V_1} + {V_2}}}{2} = \frac{{18 + 6}}{2} = 12{\rm{l}}}\end{array}} \right.\)
\(\frac{{pV}}{{{T_{\max }}}} = nR \Rightarrow \frac{{9.12}}{{{T_{\max }}}} = 2.0,082 \Rightarrow {T_{\max }} \approx 658,5\;{\rm{K}}\)
\({W_d} = \frac{3}{2}kT = \frac{3}{2} \cdot 1,38 \cdot {10^{ - 23}} \cdot 658,5 \approx 1,36 \cdot {10^{ - 20}}J\)
Trả lời ngắn: 1,36
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.