Gọi \(I\) là một điểm tùy ý nằm trên parabol \(y = {x^2}\) và \(N\) là điểm đối xứng với điểm \(O\) (gốc tọa độ) qua điểm \(I\). Khi \(I\) di chuyển trên parabol thì \(N\) di chuyển trên đường nào?
A. Đường thẳng \(y = x\).
B. Parobol \(y = \frac{1}{2}{x^2}\).
C. Parobol \(y = 2{x^2}\).
D. Đường thẳng \(y = - 2x\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn B
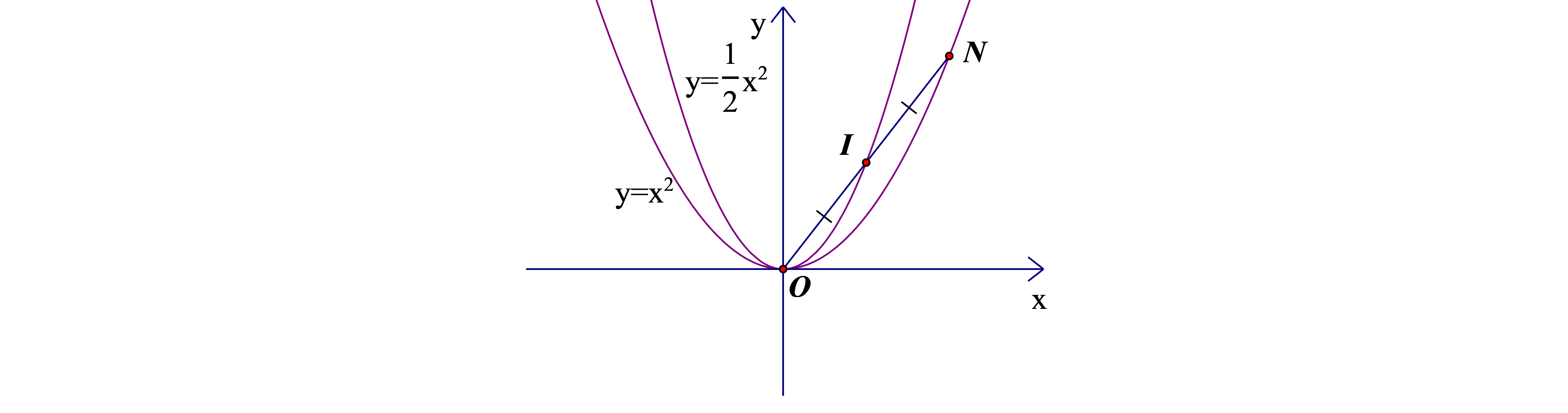
Gọi tọa độ của \(I\) là \(\left( {x;y} \right)\), tọa độ của \(N\) là \(\left( {x';y'} \right)\).
Vì \(N\) đối xứng với \(O\) qua \(I\) nên \(I\) là trung điểm của \(ON\)\( \Rightarrow x = \frac{{x'}}{2}\); \(y = \frac{{y'}}{2}\).
Điểm \(I\) thuộc parabol nên ta có \(y = {x^2}\)\( \Rightarrow \frac{{y'}}{2} = {\left( {\frac{{x'}}{2}} \right)^2}\)\( \Leftrightarrow y' = \frac{{x{'^2}}}{2}\).
Vậy điểm \(N\) di chuyển trên parabol \(y = \frac{1}{2}{x^2}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn D
Vì điểm \[M\left( {\frac{1}{2};\,\frac{{ - 1}}{2}} \right)\] thuộc đồ thị hàm số \[y = a{x^2}\left( {a \ne 0} \right)\] nên
\[\frac{{ - 1}}{2} = a.{\left( {\frac{1}{2}} \right)^2}\]\[ \Leftrightarrow a = - 2\] (thỏa mãn).
Vậy \[a = - 2\].
Câu 2
A. \(y = {x^2}\).
B. \(y = 2{x^2}\).
C. \(y = \frac{1}{2}{x^2}\).
D. \(y = - {x^2}\).
Lời giải
Chọn C
Cách 1: Parabol đã cho có dạng là đồ thị hàm số \[y = a{x^2}\left( {a > 0} \right)\].
Do parabol này đi qua điểm \[A\left( { - 2\,;\,2} \right)\] nên \[a.{\left( { - 2} \right)^2} = 2\]\[ \Leftrightarrow a = \frac{1}{2}\] ( thỏa mãn \[a > 0\]).
Vậy hàm số cần tìm là \[y = \frac{1}{2}{x^2}\].
Cách 2: Parabol đã cho có dạng là đồ thị hàm số \[y = a{x^2}\left( {a > 0} \right)\] nên ta có thể loại ngay phương án D.
Thử trực tiếp các phương án còn lại, nhận thấy hàm số có đồ thị đi qua điểm \[A\left( { - 2\,;\,2} \right)\] là \[y = \frac{1}{2}{x^2}\].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\left( { - 4;\,\, - 4} \right);\,\,\left( { - 2;\,\, - 1} \right);\,\,\left( {0;\,\,0} \right);\,\,\left( {2;\,\, - 1} \right);\,\,\left( {4;\,\, - 4} \right).\)
B. \(\left( { - 4;\,\,4} \right);\,\,\left( { - 2;\,\, - 1} \right);\,\,\left( {0;\,\,0} \right);\,\,\left( {2;\,\, - 1} \right);\,\,\left( {4;\,\, - 4} \right).\)
C. \(\left( { - 4;\,\, - 4} \right);\,\,\left( { - 2;\,\,1} \right);\,\,\left( {0;\,\,0} \right);\,\,\left( {2;\,\, - 1} \right);\,\,\left( {4;\,\, - 4} \right).\)
D. \(\left( { - 4;\,\, - 4} \right);\,\,\left( {2;\,\, - 1} \right);\,\,\left( {0;\,\,0} \right);\,\,\left( {2;\,\,1} \right);\,\,\left( {4;\,\, - 4} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\left( {\sqrt 3 ;\, - 6} \right);\,\,\left( { - \sqrt 3 ;\, - 6} \right).\)
B. \(\left( { - 6;\,\sqrt 3 } \right);\,\,\left( { - 6;\, - \sqrt 3 } \right).\)
C. \(\left( {\sqrt 3 ;\, - 6} \right).\)
D. \(\left( { - 72; - 6} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(m < - 2.\)
B. \(m \le - 2.\)
C. \(m > - 2.\)
D. \(m \ge - 2.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(m = 1.\)
B. \(m = 5.\)
C. \(m = 2.\)
D. \(m = 3.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập