15 câu trắc nghiệm Toán 9 Cánh diều Bài 1. Hàm số y = ax^2 (a ≠ 0) có đáp án
46 người thi tuần này 4.6 657 lượt thi 13 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi Giữa kì 2 Toán 9 trường THCS Ba Đình (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Mai Dịch (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Chương Dương (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Ban Mai School (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Trần Đăng Ninh (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Mạc Đĩnh Chi (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Phan Chu Trinh (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Ngô Sĩ Liên (Hà Nội) năm học 2024-2025 có đáp án
Danh sách câu hỏi:
Câu 1
A. Đồ thị hàm số nhận trục tung làm trục đối xứng.
B. Với \(a < 0\) thì đồ thị nằm phía dưới trục hoành và \(O\left( {0;0} \right)\) là điểm cao nhất của đồ thị.
C. Với \(a > 0\) thì đồ thị nằm phía trên trục hoành và \(O\left( {0;0} \right)\) là điểm cao nhất của đồ thị.
D. Với \(a > 0\) thì đồ thị nằm phía trên trục hoành và \(O\left( {0;0} \right)\) là điểm thấp nhất của đồ thị.
Lời giải
Đáp án đúng là: C
Đồ thị của hàm số \(y = a{x^2}\,\,\left( {a \ne 0} \right)\) là một đường cong, gọi là đường parabol, có các tính chất sau:
Có đỉnh là gốc tọa độ \(O\,;\)
Có trục đối xứng là \(Oy\,;\)
Nằm phía trên trục hoành nếu \(a > 0\) và nằm phía dưới trục hoành nếu \(a < 0.\)
Câu 2
A. \(\left( {0;0} \right).\)
B. \(\left( { - x;y} \right).\)
C. \(\left( {x;y} \right).\)
D. \[\left( {x; - y} \right).\]
Lời giải
Đáp án đúng là: B
Hai điểm \(\left( {x;y} \right)\) và \(\left( { - x;y} \right)\) đối xứng nhau qua trục tung \(Oy.\)
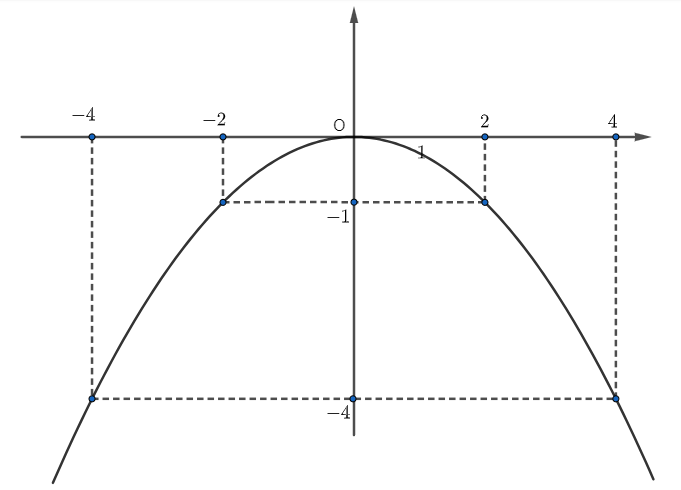
Câu 3
A. \(a = - 1.\)
B. \[a = 1.\]
C. \(a < 0.\)
</>
D. \(a > 0.\)
Lời giải
Đáp án đúng là: C
Đồ thị hàm số trong hình vẽ trên có dạng parabol nên \(y = a{x^2}\,\,\left( {a \ne 0} \right)\).
Vì đồ thị hàm số đi nằm phía dưới trục hoành nên \(a < 0.\)
Câu 4
A. \(\left( { - 1\,;\, - 3} \right).\)
B. \[\left( {4\,;\,\,12} \right).\]
C. \(\left( { - 2\,;\,\, - 6} \right).\)
D. \(\left( {1\,;\,\,3} \right).\)
Lời giải
Đáp án đúng là: D
Điểm \(\left( { - 1\,;\,\, - 3} \right)\) không thuộc đồ thị hàm số \(y = 3{x^2}\) vì \(3{\left( { - 1} \right)^2} = 3 \ne - 3.\)
Điểm \(\left( {4\,;\,\,12} \right)\) không thuộc đồ thị hàm số \(y = 3{x^2}\) vì \({3.4^2} = 48 \ne 12.\)
Điểm \(\left( { - 2\,;\,\, - 6} \right)\) không thuộc đồ thị hàm số \(y = 3{x^2}\) vì \(2.{\left( { - 2} \right)^2} = 8 \ne - 6.\)
Điểm \(\left( {1\,;\,\,3} \right)\) thuộc đồ thị hàm số \(y = 3{x^2}\) vì \({3.1^2} = 3.\)
Câu 5
A. \(m = - 1.\)
B. \(m = 1.\)
C. \(m = 0.\)
D. \(m = 2.\)
Lời giải
Đáp án đúng là: A
Hàm số \(y = \left( {m + 2} \right){x^2}\) có đồ thị đi qua điểm \(\left( { - 1\,;\,\,3} \right)\) nên ta có:
\(3 = \left( {m + 2} \right){\left( { - 1} \right)^2}\)
\(m + 2 = 3\)
\(m = 1.\)
Vậy để đồ thị hàm số \(y = \left( {m + 2} \right){x^2}\) đi qua điểm \(\left( { - 1\,;\,\,3} \right)\) thì \(m = 1.\)
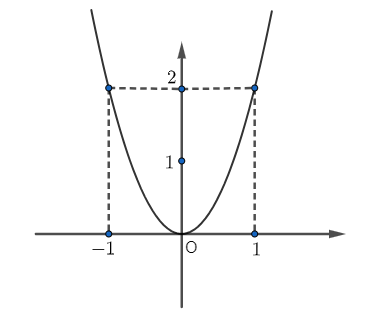
Câu 6
A. \(\left( { - 4;\,\, - 4} \right);\,\,\left( { - 2;\,\, - 1} \right);\,\,\left( {0;\,\,0} \right);\,\,\left( {2;\,\, - 1} \right);\,\,\left( {4;\,\, - 4} \right).\)
B. \(\left( { - 4;\,\,4} \right);\,\,\left( { - 2;\,\, - 1} \right);\,\,\left( {0;\,\,0} \right);\,\,\left( {2;\,\, - 1} \right);\,\,\left( {4;\,\, - 4} \right).\)
C. \(\left( { - 4;\,\, - 4} \right);\,\,\left( { - 2;\,\,1} \right);\,\,\left( {0;\,\,0} \right);\,\,\left( {2;\,\, - 1} \right);\,\,\left( {4;\,\, - 4} \right).\)
D. \(\left( { - 4;\,\, - 4} \right);\,\,\left( {2;\,\, - 1} \right);\,\,\left( {0;\,\,0} \right);\,\,\left( {2;\,\,1} \right);\,\,\left( {4;\,\, - 4} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left( {\sqrt 3 ;\, - 6} \right);\,\,\left( { - \sqrt 3 ;\, - 6} \right).\)
B. \(\left( { - 6;\,\sqrt 3 } \right);\,\,\left( { - 6;\, - \sqrt 3 } \right).\)
C. \(\left( {\sqrt 3 ;\, - 6} \right).\)
D. \(\left( { - 72; - 6} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(m < - 2.\)
B. \(m \le - 2.\)
C. \(m > - 2.\)
D. \(m \ge - 2.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(m = 1.\)
B. \(m = 5.\)
C. \(m = 2.\)
D. \(m = 3.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \(y = 4{x^2}.\)
B. \[y = \frac{1}{2}{x^2}.\]
C. \(y = \frac{1}{4}{x^2}.\)
D. \(y = 2{x^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \(y = - x + 2.\)
B. \(y = x + 2.\)
C. \(y = - x - 2.\)
D. \(y = x - 2.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \(4\sqrt 2 .\)
B. \(5\sqrt 3 .\)
C. \(4.\)
D. \(2\sqrt 2 .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.