15 câu trắc nghiệm Toán 9 Cánh diều Bài tập cuối chương V có đáp án
38 người thi tuần này 4.6 512 lượt thi 15 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi Giữa kì 2 Toán 9 trường THCS Ba Đình (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Mai Dịch (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Chương Dương (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Ban Mai School (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Trần Đăng Ninh (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Mạc Đĩnh Chi (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Phan Chu Trinh (Hà Nội) năm học 2024-2025 có đáp án
Đề thi Giữa kì 2 Toán 9 trường THCS Ngô Sĩ Liên (Hà Nội) năm học 2024-2025 có đáp án
Danh sách câu hỏi:
Câu 1
A. điểm \[H\] nằm ngoài đường tròn \[\left( {O\,;\,2{\rm{\;cm}}} \right).\]
B. điểm \[H\] nằm trên đường tròn \[\left( {O\,;\,2{\rm{\;cm}}} \right).\]
C. điểm \[H\] nằm trong đường tròn \[\left( {O\,;\,2{\rm{\;cm}}} \right).\]
D. điểm \[H\] trùng tâm \[O\] của đường tròn \[\left( {O\,;\,2{\rm{\;cm}}} \right).\]
Lời giải
Đáp án đúng là: C
Do \[OH < 2{\rm{\;cm}}\] nên điểm \[H\] nằm trong đường tròn \[\left( {O\,;\,2{\rm{\;cm}}} \right).\]
Vậy ta chọn phương án C.
Câu 2
A. lớn nhất.
B. nhỏ nhất.
C. bằng \[100{\rm{\;cm}}.\]
D. bằng tổng hai dây bất kì.
Lời giải
Đáp án đúng là: A
Ta có trong một đường tròn, đường kính là dây cung lớn nhất.
Vì vậy ta điền như sau: “Trong các dây của một đường tròn, đường kính là dây có độ dài lớn nhất”.
Vậy ta chọn phương án A.
Câu 3
A. \[5\pi {\rm{\;c}}{{\rm{m}}^2}.\]
B. \[3\pi {\rm{\;c}}{{\rm{m}}^2}.\]
C. \[1,5\pi {\rm{\;c}}{{\rm{m}}^2}.\]
D. \[2\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Lời giải
Đáp án đúng là: A
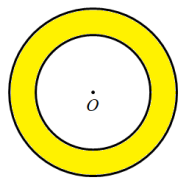
Diện tích hình vành khuyên giới hạn bởi hai đường tròn đồng tâm \[\left( {O;2{\rm{\;cm}}} \right)\] và \[\left( {O;3{\rm{\;cm}}} \right)\] là:
\[{S_v} = \pi \left( {{R^2} - {r^2}} \right) = \pi \left( {{3^2} - {2^2}} \right) = 5\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Vậy ta chọn phương án A.
Câu 4
A. \[d \equiv OA.\]
B. \[d \bot OA\] tại \[O.\]
C. \[d\,{\rm{//}}\,OA.\]
D. \[d \bot OA\] tại \[A.\]
Lời giải
Đáp án đúng là: D
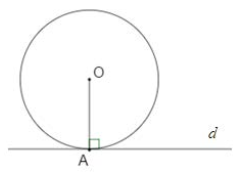
Ta có đường thẳng \[d\] là tiếp tuyến của đường tròn \[\left( O \right)\] tại \[A\] nên \[d \bot OA\] tại \[A,\] với \[A\] là tiếp điểm.
Vậy ta chọn phương án D.
Câu 5
A. Tiếp xúc trong.
B. Tiếp xúc ngoài.
C. Nằm ngoài nhau.
D. Cắt nhau.
Lời giải
Đáp án đúng là: A

Vì đường tròn \[\left( {O'} \right)\] có đường kính \[OA\] nên \[O'\] là trung điểm \[OA.\]
Do đó \[OO' = O'A = \frac{{OA}}{2}.\]
Đặt \[R = OA\] và \[R' = O'A = \frac{{OA}}{2}.\] Suy ra \[R > R'.\]
Ta có \[OA - \frac{{OA}}{2} = \frac{{OA}}{2}.\] Suy ra \[R - R' = OO',\] với \[R > R'.\]
Khi đó hai đường tròn \[\left( {O;OA} \right)\] và \[\left( {O';\frac{{OA}}{2}} \right)\] tiếp xúc trong.
Vậy ta chọn phương án A.
Câu 6
A. \(OA \bot BC\).
B. \(OA\) là đường trung trực của \(BC\).
C. \(AB = AC\).
D. \(OA \bot BC\) tại trung điểm của \(AO\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Tam giác cân.
B. Tam giác vuông.
C. Tam giác vuông cân.
D. Tam giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. đựng nhau.
B. tiếp xúc ngoài.
C. ở ngoài nhau.
D. cắt nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \[8,5{\rm{\;cm}}.\]
B. \[17{\rm{\;cm}}.\]
C. \[12,7{\rm{\;cm}}.\]
D. \[6,3{\rm{\;cm}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \[\widehat {AOD} = 3\widehat {ACD}.\]
C.
D. \[\widehat {ACD} = 30^\circ .\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \[\frac{{4\pi }}{3}{\rm{\;cm}}.\]
B. \[\frac{{5\pi }}{3}{\rm{\;cm}}.\]
C. \[\frac{{7\pi }}{3}{\rm{\;cm}}.\]
D. \[\frac{{8\pi }}{3}{\rm{\;cm}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \[\widehat {CBO'} = 90^\circ .\]
B. \[AC = CB.\]
C. \[CA,CB\] là hai tiếp tuyến của \[\left( {O'} \right).\]
D. Cả A, B, C đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Không có hình nào biểu diễn cặp cồng chiêng có hai đường tròn tiếp xúc trong với nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. \[\frac{{25\pi }}{2}{\rm{\;d}}{{\rm{m}}^2}.\]
B. \[\frac{{25\pi }}{{48}}{\rm{\;d}}{{\rm{m}}^2}.\]
C. \[\frac{{25\pi }}{4}{\rm{\;d}}{{\rm{m}}^2}.\]
D. \[\frac{{25\pi }}{{12}}{\rm{\;d}}{{\rm{m}}^2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. Chỉ (i) đúng.
B. Chỉ (ii) đúng.
C. Cả (i), (ii) đều đúng.
D. Cả (i), (ii) đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.