15 câu trắc nghiệm Toán 9 Cánh diều Ôn tập chương VIII có đáp án
58 người thi tuần này 4.6 796 lượt thi 15 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi giữa kì 1 Toán 9 năm 2026-2027 THCS&THPT M.V. Lô-Mô-Nô-Xốp (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 9 năm 2026-2027 Hệ thống giáo dục Newton-Pascal (có đáp án)
Đề thi giữa kì 1 Toán 9 năm 2025-2026 THCS Thực Nghiệm Khoa học Giáo dục (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 9 năm 2025-2026 THCS Nguyễn Trường Tộ (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 9 năm 2025-2026 THCS Hoàng Hoa Thám (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 9 năm 2025-2026 THCS Giảng Võ (Hà Nội) có đáp án
Đề thi giữa kì 1 Toán 9 năm 2025-2026 THCS Lê Quý Đôn (Hà Nội) có đáp án
Trắc nghiệm Tổng hợp Toán năm 2024 có đáp án - Phần 19
Danh sách câu hỏi:
Câu 1/15
A. Trọng tâm của tam giác đều vừa là tâm đường tròn ngoại tiếp, vừa là tâm đường tròn nội tiếp tam giác đều đó.
B. Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác của tam giác đó.
C. Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
D. Đường tròn ngoại tiếp một tam giác là đường tròn đi qua nhiều nhất là ba đỉnh của tam giác đó.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
Phương án A, B, C đúng.
Phương án D sai. Sửa lại: Đường tròn ngoại tiếp một tam giác là đường tròn đi qua cả ba đỉnh của tam giác đó.
Vậy ta chọn phương án D.
Câu 2/15
A. Tiếp xúc tất cả các cạnh của đa giác đó.
B. Đi qua tất cả các đỉnh của đa giác đó.
C. Cắt tất cả các cạnh của đa giác đó.
D. Đi qua tâm của đa giác đó.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: B
Đường tròn ngoại tiếp đa giác là đường tròn đi qua tất cả các đỉnh của đa giác đó.
Câu 3/15
A. Hình thang, hình chữ nhật.
B. Hình thang cân, hình bình hành.
C. Hình thoi, hình vuông.
D. Hình thang, hình chữ nhật, hình vuông.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: C
Hình thoi và hình vuông có đường chéo cắt nhau tại trung điểm mỗi đường nên nội tiếp đường tròn có tâm là giao điểm hai đường chéo và bán kính bằng nửa đường chéo.
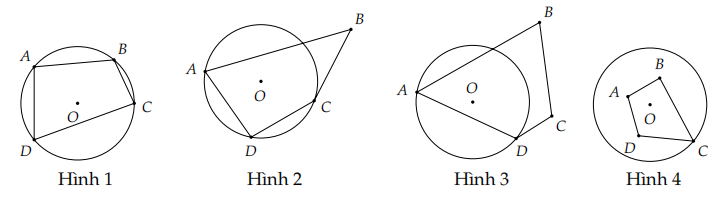
Câu 4/15
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
Ta thấy trên hình 1, các điểm \[A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D\] đều nằm trên đường tròn \[\left( O \right)\] nên tứ giác \[ABCD\] trên hình 1 là tứ giác nội tiếp.
Câu 5/15
A. tứ giác có bốn đỉnh nằm trên đường tròn đó;
B. tứ giác có nhiều nhất bốn đỉnh nằm trên đường tròn đó;
C. tứ giác có tổng số đo hai góc đối nhau bằng 90°;
D. tứ giác có ba đỉnh nằm trên đường tròn đó.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
Tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên đường tròn đó.
Vậy ta chọn phương án A.
Câu 6/15
A. \(90^\circ \).
B. \(180^\circ \).
C. \(110^\circ \).
D. \(120^\circ \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
Tứ giác \[MNPQ\] nội tiếp đường tròn nên \(\widehat M + \widehat P = 180^\circ \) hay \(\widehat P = 180^\circ - \widehat M = 180^\circ - 90^\circ = 90^\circ \).
Câu 7/15
A. \(120^\circ \).
B. \(60^\circ \).
C. \(140^\circ \).
D. \(80^\circ \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8/15
A. \[1{\rm{ dm}}\] và \[1{\rm{ dm}}\].
B. \[0,5\,\,{\rm{dm}}\] và \[0,5\,\,{\rm{dm}}\].
C. \[0,5\,\,{\rm{dm}}\] và \[1{\rm{ dm}}\].
D. \[1{\rm{ dm}}\] và \[0,5\,\,{\rm{dm}}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9/15
A. \(110^\circ \).
B. \(70^\circ \).
C. \(140^\circ \).
D. \(290^\circ \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10/15
A. 95° và 120°.
B. 60° và 95°.
C. 30° và 60°.
D. 95° và 60°.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
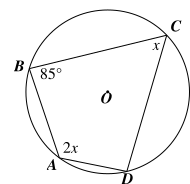
Câu 11/15
A. \[\widehat {AOD}\, = 80^\circ .\]
B. \[\widehat {AOD}\, = 70^\circ .\]
C. \[\widehat {AOD}\, = 60^\circ .\]
D. \[\widehat {AOD}\, = 50^\circ .\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12/15
A. \(60^\circ \).
B. \(70^\circ \).
C. \(80^\circ \).
D. \(90^\circ \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
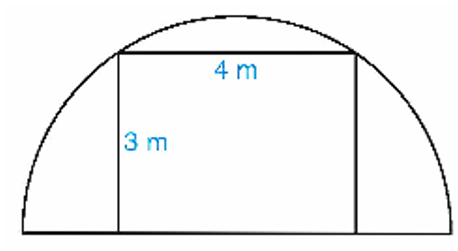
Câu 13/15
![Người ta làm một khung gỗ hình tam giác đều đặt vừa khít một chiếc đồng hồ hình tròn có đường kính \[40{\rm{ cm}}.\] Độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu (làm tr (ảnh 1)](https://video.vietjack.com/upload2/images/1731559220/1731559937-image8.png)
A. \[69,28\,\,{\rm{cm}}.\]
B. \[69,18\,\,{\rm{cm}}.\]
C. \[60,28\,\,{\rm{cm}}.\]
D. \[66,28\,\,{\rm{cm}}.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14/15
A. \[\widehat {MHN} + \widehat {ABC} = 180^\circ .\]
B. \[\widehat {AHC} = \widehat {ADC}\,.\]
C. \[\widehat {ADC} = \widehat {BAM} + 90^\circ .\]
D. Cả A, B, C đều đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15/15
A. \[11,66\,\,{\rm{cm}}.\]
B. \[11,33\,\,{\rm{cm}}.\]
C. \[12,05\,\,{\rm{cm}}.\]
D. \[11,26\,\,{\rm{cm}}.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 9/15 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập