III. Vận dụng

Người ta làm một khung gỗ hình tam giác đều đặt vừa khít một chiếc đồng hồ hình tròn có đường kính \[40{\rm{ cm}}.\]

Độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu (làm tròn kết quả đến hàng phần trăm)?

Đáp án đúng là: B

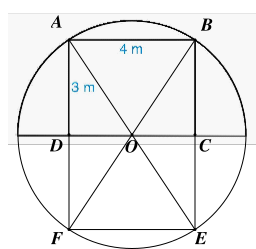
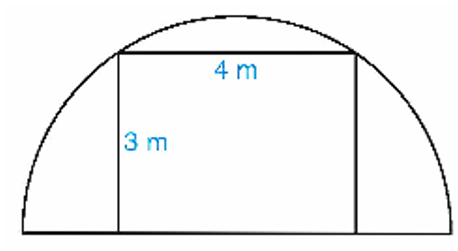
Gọi \[ABCD\] là khung cổng hình chữ nhật.

Vẽ hình chữ nhật \[ABEF\] (hình vẽ) và \[O\] là giao điểm của hai đường chéo \[AE,{\rm{ }}BF.\]

Khi đó ta có \[AF = 2AD = 2 \cdot 3 = 6{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\]

Tam giác \[ABF\] vuông tại A, theo định lí Pythagore, ta có:

\[B{F^2} = A{F^2} + A{B^2} = {6^2} + {4^2} = 52.\]

Do đó \[BF = \sqrt {52} = 2\sqrt {13} \,\,\left( {{\rm{cm}}} \right).\]

Vì vậy bán kính đường tròn ngoại tiếp hình chữ nhật \[ABEF\] là: \[R = \frac{{BF}}{2} = \sqrt {13} \,\,\left( {{\rm{cm}}} \right).\]

Chu vi đường tròn ngoại tiếp hình chữ nhật \[ABEF\] là: \[C = 2\pi R = 2\pi \sqrt {13} \,\,\left( {{\rm{cm}}} \right).\]

Vậy chiều dài của đoạn thép dùng để làm khung nửa đường tròn là \[\frac{C}{2} = \frac{{2\pi \sqrt {13} }}{2} \approx 11,33\,\,\left( {{\rm{cm}}} \right).\]

Đáp án đúng là: C

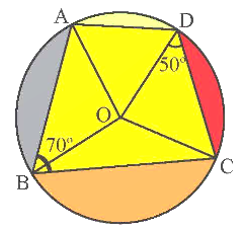
Tứ giác \[ABCD\] nội tiếp đường tròn \[\left( {O;{\rm{ }}R} \right)\] có: \[\widehat {ADC} + \widehat {ABC} = 180^\circ \] (tổng hai góc đối của tứ giác nội tiếp).

Suy ra \[\widehat {ADC} = 180^\circ - \widehat {ABC} = 180^\circ - 70^\circ = 110^\circ .\]

Ta có \[\widehat {ADO} + \widehat {ODC} = \widehat {ADC}\,.\]

Suy ra \[\widehat {ADO} = \widehat {ADC} - \widehat {ODC} = 110^\circ - 50^\circ = 60^\circ .\]

Tam giác \[OAD\] cân tại \[O\] (do \[OA = OD = R\]) có \[\widehat {ADO} = 60^\circ \] nên \[\Delta OAD\] là tam giác đều. Do đó \[\widehat {AOD}\, = 60^\circ .\]