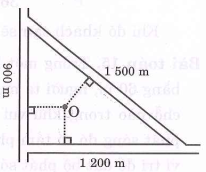
Ba vị trí \({\rm{A}},{\rm{B}},{\rm{C}}\) ở một công viên là ba đỉnh của một tam giác đều cạnh 15 m . Người ta cần chọn vị trí O cách đều ba vị trí \({\rm{A}},{\rm{B}},{\rm{C}}\) để làm một cột đền. Tính khoảng cách từ vị trí O đến mỗi vị trí \({\rm{A}},{\rm{B}},{\rm{C}}\).
Ba vị trí \({\rm{A}},{\rm{B}},{\rm{C}}\) ở một công viên là ba đỉnh của một tam giác đều cạnh 15 m . Người ta cần chọn vị trí O cách đều ba vị trí \({\rm{A}},{\rm{B}},{\rm{C}}\) để làm một cột đền. Tính khoảng cách từ vị trí O đến mỗi vị trí \({\rm{A}},{\rm{B}},{\rm{C}}\).
Câu hỏi trong đề: 6 bài tập Toán thực tế (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
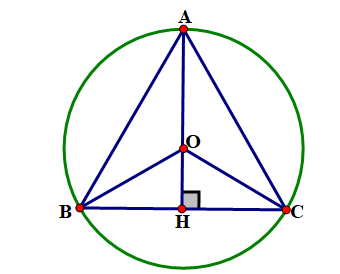
Gọi O là vị trí cách đều ba vị trí \({\rm{A}},{\rm{B}},{\rm{C}}\) nên O là tâm đường tròn ngoại tiếp tam giác ABC (giao điểm của ba đường trung trực).
Do đều (gt) nên O đồng thời là trực tâm và trọng tâm của tam giác hay AH là đường cao của tam giác ABC
đều cạnh 15 m .\( \Rightarrow {\rm{AH}} = \frac{{15\sqrt 3 }}{2}(\;{\rm{m}})\) vì AH đồng thời là trung tuyến của có trọng tâm O\( \Rightarrow {\rm{OA}} = \frac{2}{3}{\rm{AH}} = \frac{2}{3} \cdot \frac{{15\sqrt 3 }}{2} = 5\sqrt 3 (\;{\rm{m}})\).
Vậy khoảng cách từ vị trí O đến mỗi vị trí \({\rm{A}},{\rm{B}},{\rm{C}}\) là \(5\sqrt 3 (\;{\rm{m}})\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
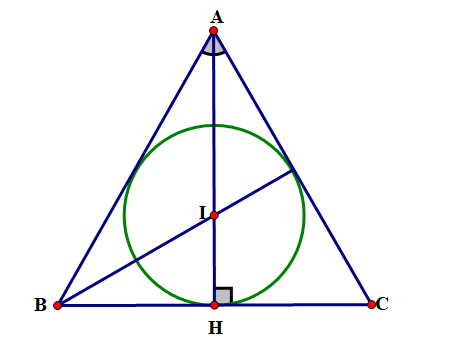
Gọi I là tâm của đường tròn nội tiếp tam giác đều ABC .
Kẻ đường cao AH , khi đó tâm I của đường tròn nội tiếp (giao điểm của ba đường phân giác cũng là trọng tâm).
Ta có AH là đường trung tuyến\( \Rightarrow {\rm{H}}\)là trung điểm của BC hay \({\rm{BH}} = {\rm{CH}} = \frac{{{\rm{BC}}}}{2} = \frac{{12}}{2} = 6\) (m).
Xét tam giác BHI vuông tại H . Có \({\rm{BH}} = 6\;{\rm{cm}}\) và
Theo định lí về hệ thức lượng trong tam giác vuông, ta có:
Vậy bán kính của phần đất trồng hoa là \({\rm{r}} = 2\sqrt 3 (\;{\rm{m}})\)
Do đó diện tích phần đất trồng hoa là \({\rm{S}} = \pi \cdot {(2\sqrt 3 )^2} = 12\pi \left( {\;{{\rm{m}}^2}} \right)\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
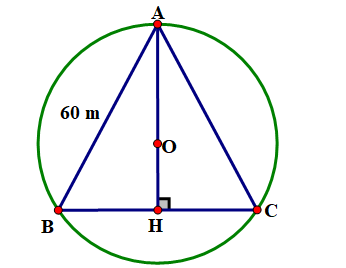
Vì \(O\) cách đều 3 đỉnh của tam giác \(ABC\) nên \(O\) là tâm đường tròn ngoại tiếp tam giác đều \(ABC\).
Gọi \(a\left( {cm} \right)\) là độ dài cạnh của tam giác đều \(ABC{\rm{ }}\left( {a > 0} \right)\).
Ta có bán kính đường tròn ngoại tiếp tam giác đều là \(60cm\).
Nên \(R = \frac{{a\sqrt 3 }}{3} \Rightarrow 60 = \frac{{a\sqrt 3 }}{3} \Leftrightarrow a\sqrt 3 = 180 \Leftrightarrow a \approx 104\) (nhận).
Vậy khoảng cách từ \(A\) đến \(B\) khoảng \(104m\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập