a) Tính số đường chéo của đa giác \[n\] cạnh.

b) Đa giác nào có số đường chéo bằng số cạnh?

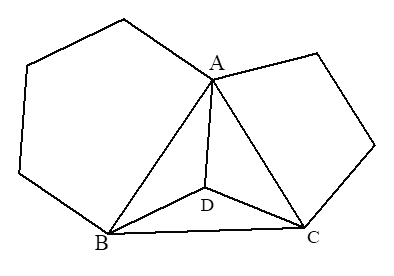
Theo công thức tính góc của đa giác đều, ta có:

\(\widehat {ADB} = \frac{{\left( {6 - 2} \right){{.180}^0}}}{6} = {120^0} \Rightarrow \widehat {DAB} = \widehat {DBA} = {30^0};\)

\(\widehat {ADC} = \frac{{\left( {5 - 2} \right){{180}^0}}}{5} = {108^0} \Rightarrow \widehat {DAC} = \widehat {DCA} = {36^0};\)  

Suy ra \(\widehat {BDC} = {360^0} - {120^0} - {108^0} = {132^0}\) .

Ta có ∆BDC \[\left( {DB = DC} \right)\] cân tại D. Do đó \(\widehat {DBC} = \widehat {DCB} = \frac{{{{180}^0} - {{132}^0}}}{2} = {24^0}\) .

Suy ra \(\widehat {BAC} = {30^0} + {36^0} = {66^0};\widehat {{\rm{ }}ABC} = {30^0} + {24^0} = {54^0};\widehat {{\rm{ }}BCA} = {24^0} + {36^0} = {60^0}\)

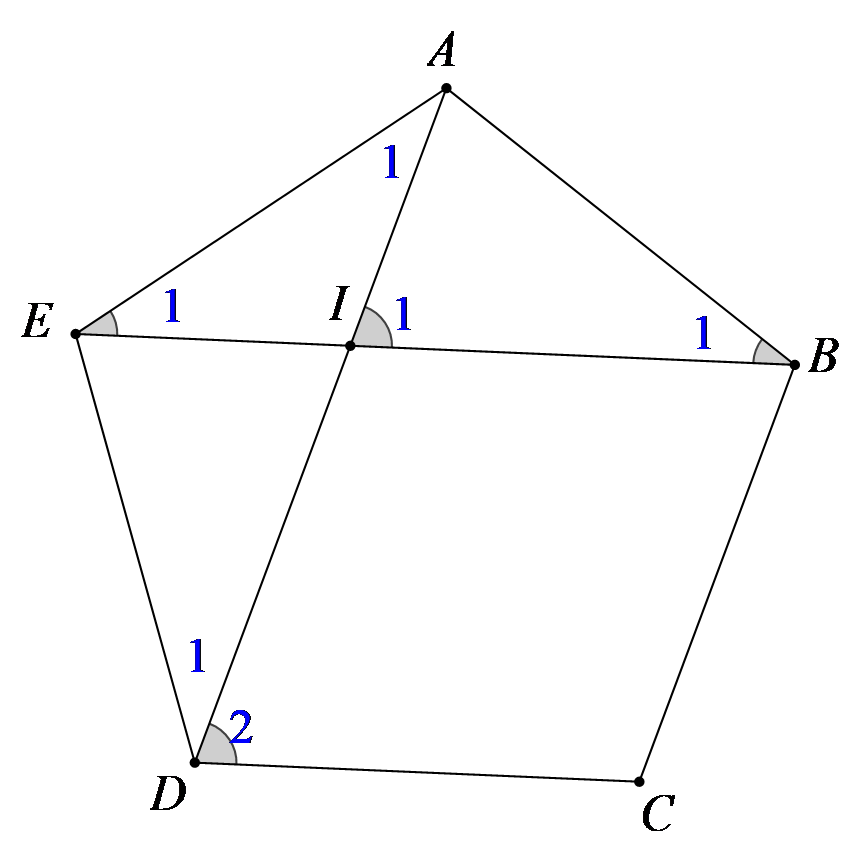
a) Ta có mỗi góc trong của ngũ giác đều có số đo là \(108^\circ \) hay \[\widehat {AED} = 108^\circ \];  Tam giác \[AED\]cân tại \[E\]từ đó \(\widehat {{A_1}} = \widehat {{D_1}} = 36^\circ \); Tương tự tính được \(\widehat {{B_1}} = \widehat {{E_1}} = 36^\circ  = \widehat {{D_1}}\)

Vậy \(\widehat {{I_1}} = \widehat {{E_1}} + \widehat {{A_1}} = 72^\circ \) (góc ngoài của tam giác \(EAI\)) và \({D_2} = \widehat {EDC} - \widehat {{D_1}} = 108^\circ  - 36^\circ  = 72^\circ \). Vậy \(\widehat {{D_2}} = \widehat {{I_1}}\) mà hai góc này ở vị trí đồng vị suy ra \[IB//DC\]. Chứng minh tương tự ta có \[DI//BC\] hay \(DIBC\) là hình bình hành.

b) Xét tam giác \(AIE\) và tam giác \(EAD\), ta có

   + Góc \(A\) chung;

   + \(\widehat {AEI} = \widehat {ADE}\).

\( \Rightarrow \Delta AIE\~\Delta AED(\;{\rm{g}} - {\rm{g}})\)suy ra \(\frac{{AI}}{{AE}} = \frac{{AE}}{{AD}}\) suy ra \(AI \cdot AD = A{E^2} \cdot B{C^2} = D{I^2}\)