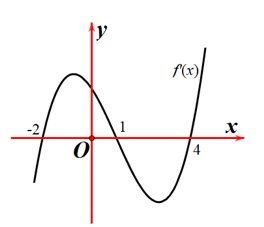
Đậu đỏ là một loại thực phẩm quen thuộc trong bữa ăn của người Việt Nam. Ngoài giá trị dinh dưỡng cao, đậu đỏ còn có nhiều công dụng tuyệt vời cho sức khỏe và sắc đẹp như: Chống ôxy hóa, giúp cơ bắp con người khỏe mạnh, tăng cường sức khỏe cho tim mạch con người, lợi ích hệ tiêu hóa, bổ thận, cung cấp vitamin bổ dưỡng cho cơ thể, đào thải độc tố, giải độc, tốt cho hệ miễn dịch, giúp huyết áp ổn định, da đẹp. Cây đậu đỏ khi trồng có chiều cao 6 cm. Khảo sát cho thấy độ cao tính bằng centimet của cây đậu đỏ tại thời điểm \(t\) kể từ khi được trồng được cho bởi hàm số \(h\left( t \right) = - 0,005{t^4} + b{t^3} + c\) (Trong đó \(b,c \in \mathbb{R}\)), với \(t\) tính theo tuần. Giả sử \(h'\left( t \right)\) là tốc độ tăng chiều cao của cây đậu đỏ sau khi trồng. (Đơn vị của \(h'\left( t \right)\) là centimet/tuần). Biết \(h'\left( 5 \right) = 5\). (Hình bên dưới mô tả hạt và cây đậu đỏ). Xét tính đúng, sai của các mệnh đề sau:
Đậu đỏ là một loại thực phẩm quen thuộc trong bữa ăn của người Việt Nam. Ngoài giá trị dinh dưỡng cao, đậu đỏ còn có nhiều công dụng tuyệt vời cho sức khỏe và sắc đẹp như: Chống ôxy hóa, giúp cơ bắp con người khỏe mạnh, tăng cường sức khỏe cho tim mạch con người, lợi ích hệ tiêu hóa, bổ thận, cung cấp vitamin bổ dưỡng cho cơ thể, đào thải độc tố, giải độc, tốt cho hệ miễn dịch, giúp huyết áp ổn định, da đẹp. Cây đậu đỏ khi trồng có chiều cao 6 cm. Khảo sát cho thấy độ cao tính bằng centimet của cây đậu đỏ tại thời điểm \(t\) kể từ khi được trồng được cho bởi hàm số \(h\left( t \right) = - 0,005{t^4} + b{t^3} + c\) (Trong đó \(b,c \in \mathbb{R}\)), với \(t\) tính theo tuần. Giả sử \(h'\left( t \right)\) là tốc độ tăng chiều cao của cây đậu đỏ sau khi trồng. (Đơn vị của \(h'\left( t \right)\) là centimet/tuần). Biết \(h'\left( 5 \right) = 5\). (Hình bên dưới mô tả hạt và cây đậu đỏ). Xét tính đúng, sai của các mệnh đề sau:
Quảng cáo
Trả lời:
a) Ta có \[h'\left( t \right) = \left( { - 0,005{t^4} + b{t^3} + c} \right)' = - 0,02{t^3} + 3b{t^2}\].
Mà \[h'\left( 5 \right) = 5\]\[ \Leftrightarrow - 0,{02.5^3} + 3b{.5^2} = 5 \Leftrightarrow b = \frac{{5 + 0,{{02.5}^3}}}{{{{3.5}^2}}} = 0,1\].
\(h\left( 0 \right) = 6 \Leftrightarrow c = 6\).
Do vậy \(h\left( t \right) = - 0,005{t^4} + 0,1{t^3} + 6\). Đáp án a sai.
b) Với \(h\left( t \right) = - 0,005{t^4} + 0,1{t^3} + 6\) thì \(h'\left( t \right) = - 0,02{t^3} + 0,3{t^2}\).
\(h'\left( t \right) = 0 \Leftrightarrow - 0,02{t^3} + 0,3{t^2} = 0 \Leftrightarrow {t^2}\left( { - 0,02t + 0,3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 15\end{array} \right.\)
Bảng biến thiên
|
\(t\) |
0 15 \( + \infty \) |
|
\(h'\left( t \right)\) |
+ 0 - |
|
\(h\left( t \right)\) |
 
|
Từ bảng biến thiên ta thấy giai đoạn tăng trưởng của cây là từ tuần 1 đến tuần thứ 15. Do vậy đáp án b đúng.
c) Chiều cao tối đa của cây đạt được khi \(t = 15\), và độ cao lớn nhất của cây là c\(h\left( {15} \right) \approx 90,375\left( {cm} \right)\). Do vậy đáp án c sai.
d) Thời điểm cây phát triển nhanh nhất là thời điểm \[h'\left( t \right)\] đạt giá trị lớn nhất.
Ta có \(h''\left( t \right) = - 0,06{t^2} + 0,6t\)
\(h''\left( t \right) = 0 \Leftrightarrow t\left( { - 0,06t + 0,6} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 10\end{array} \right.\) (\(t = 0\) không thỏa mãn).
Chiều cao của cây tại thời điểm \(t = 10\) là \(h\left( {10} \right) = - 0,{005.10^4} + 0,{1.10^3} + 6 = 56\)(cm). Do vậy đáp án d đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 0,05.
Gọi \(\Omega \) là không gian mẫu của phép thử.
Ta có \(n\left( \Omega \right) = 9 \cdot 8 \cdot 7 \cdot 6\).
Gọi \(A\) là biến cố lấy được \(4\) quả cầu ghi các số có tổng bằng \(15\). Ta giả sử các số đó \(a\), \(b\),\(c\), \(d\).
Theo giả thiết \(a + b + c + d = 15\).
Suy ra \(\left( {a,b,c,d} \right) \in \left\{ {\left( {1;2;3;9} \right),\left( {1,2,4,8} \right),\left( {1,2,5,7} \right),\left( {1,3,5,6} \right),\left( {1,3,4,7} \right),\left( {2,3,4,6} \right)} \right\}\)
\( \Rightarrow n\left( A \right) = 6 \times 4!\).
Vậy xác suất cẩn tính \(P\left( A \right) = \frac{{6 \times 4!}}{{9 \times 8 \times 7 \times 6}} \approx 0,05\).
Lời giải
Đáp án: 8,64.
Ta có: \(\overrightarrow {DA} = \left( { - 3;0;0} \right)\), \(\overrightarrow {DB} = \left( {0; - 4;0} \right)\) và \(\overrightarrow {DC} = \left( {0;0; - 5} \right)\).
Dễ thấy: \[\left\{ \begin{array}{l}\overrightarrow {DA} .\overrightarrow {DB} = 0 \Rightarrow DA \bot DB\\\overrightarrow {DB} .\overrightarrow {DC} = 0 \Rightarrow DB \bot DC\\\overrightarrow {DC} .\overrightarrow {DA} = 0 \Rightarrow DC \bot DA\end{array} \right.\] nên các điểm \(A\left( {0;4;5} \right)\), \(B\left( {3;0;5} \right)\), \(C\left( {3;4;0} \right)\), \(D\left( {3;4;5} \right)\) là các đỉnh của một hình hộp chữ nhật với \(DA = 3\), \(DB = 4\) và \(DC = 5\).
Gọi \(S = d\left( {A,MD} \right) + d\left( {B,MD} \right) + d\left( {C,MD} \right)\).
Ta có \(d\left( {C,MD} \right) = DC = 5\) nên \(S\) lớn nhất khi \(d\left( {A,MD} \right) + d\left( {B,MD} \right)\) lớn nhất.
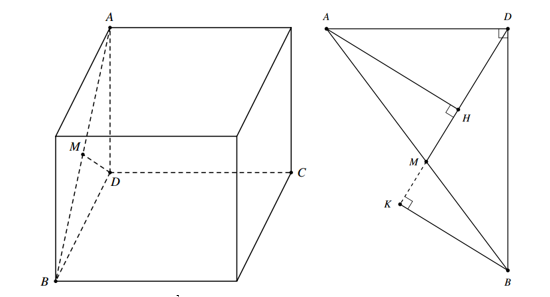
Xét \(\Delta DAB\) trong mặt phẳng \(\left( {DAB} \right)\): \(d\left( {A,MD} \right) + d\left( {B,MD} \right) \le AM + BM = AB\).
Dấu bằng xảy ra khi \(M\) là hình chiếu của \(D\) lên \(AB\).
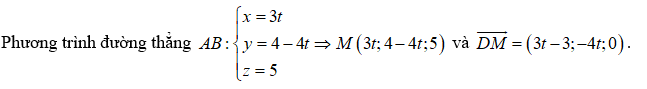
Do \[DM \bot AB \Rightarrow \overrightarrow {DM} .\overrightarrow {AB} = 0 \Rightarrow \left( {3t - 3} \right) \times 3 - 4t \times \left( { - 4} \right) = 0 \Leftrightarrow t = \frac{9}{{25}} \Rightarrow M\left( {\frac{{27}}{{25}};\frac{{64}}{{25}};5} \right)\].
Vậy \[a + b + c = \frac{{27}}{{25}} + \frac{{64}}{{25}} + 5 = 8,64\].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.