Hệ thống định vị toàn cầu GPS là một hệ thống cho phép xác định vị trí của một vật thể trong không gian. Trong cùng một thời điểm vị trí của điểm \(M\) trong không gian sẽ được xác định bởi bốn vệ tinh cho trước nhờ các bộ thu phát tín hiệu đặt trên các vệ tinh. Giả sử trong không gian với hệ tọa độ \(Oxyz\), có bốn vệ tinh lần lượt đặt tại các điểm \(A\left( {0;4;5} \right)\), \(B\left( {3;0;5} \right)\), \(C\left( {3;4;0} \right)\), \(D\left( {3;4;5} \right)\) và vị trí \(M\left( {a;b;c} \right)\) trên đoạn thẳng \(AB\) thỏa mãn tổng khoảng cách từ các điểm \(A\), \(B\), \(C\) đến đường thẳng \(MD\) lớn nhất. Khi đó giá trị \(a + b + c\) bằng bao nhiêu?
Quảng cáo
Trả lời:
Đáp án:
Đáp án: 8,64.
Ta có: \(\overrightarrow {DA} = \left( { - 3;0;0} \right)\), \(\overrightarrow {DB} = \left( {0; - 4;0} \right)\) và \(\overrightarrow {DC} = \left( {0;0; - 5} \right)\).
Dễ thấy: \[\left\{ \begin{array}{l}\overrightarrow {DA} .\overrightarrow {DB} = 0 \Rightarrow DA \bot DB\\\overrightarrow {DB} .\overrightarrow {DC} = 0 \Rightarrow DB \bot DC\\\overrightarrow {DC} .\overrightarrow {DA} = 0 \Rightarrow DC \bot DA\end{array} \right.\] nên các điểm \(A\left( {0;4;5} \right)\), \(B\left( {3;0;5} \right)\), \(C\left( {3;4;0} \right)\), \(D\left( {3;4;5} \right)\) là các đỉnh của một hình hộp chữ nhật với \(DA = 3\), \(DB = 4\) và \(DC = 5\).
Gọi \(S = d\left( {A,MD} \right) + d\left( {B,MD} \right) + d\left( {C,MD} \right)\).
Ta có \(d\left( {C,MD} \right) = DC = 5\) nên \(S\) lớn nhất khi \(d\left( {A,MD} \right) + d\left( {B,MD} \right)\) lớn nhất.
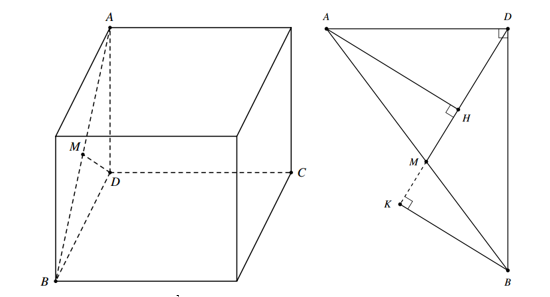
Xét \(\Delta DAB\) trong mặt phẳng \(\left( {DAB} \right)\): \(d\left( {A,MD} \right) + d\left( {B,MD} \right) \le AM + BM = AB\).
Dấu bằng xảy ra khi \(M\) là hình chiếu của \(D\) lên \(AB\).
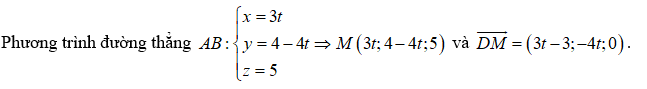
Do \[DM \bot AB \Rightarrow \overrightarrow {DM} .\overrightarrow {AB} = 0 \Rightarrow \left( {3t - 3} \right) \times 3 - 4t \times \left( { - 4} \right) = 0 \Leftrightarrow t = \frac{9}{{25}} \Rightarrow M\left( {\frac{{27}}{{25}};\frac{{64}}{{25}};5} \right)\].
Vậy \[a + b + c = \frac{{27}}{{25}} + \frac{{64}}{{25}} + 5 = 8,64\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 0,05.
Gọi \(\Omega \) là không gian mẫu của phép thử.
Ta có \(n\left( \Omega \right) = 9 \cdot 8 \cdot 7 \cdot 6\).
Gọi \(A\) là biến cố lấy được \(4\) quả cầu ghi các số có tổng bằng \(15\). Ta giả sử các số đó \(a\), \(b\),\(c\), \(d\).
Theo giả thiết \(a + b + c + d = 15\).
Suy ra \(\left( {a,b,c,d} \right) \in \left\{ {\left( {1;2;3;9} \right),\left( {1,2,4,8} \right),\left( {1,2,5,7} \right),\left( {1,3,5,6} \right),\left( {1,3,4,7} \right),\left( {2,3,4,6} \right)} \right\}\)
\( \Rightarrow n\left( A \right) = 6 \times 4!\).
Vậy xác suất cẩn tính \(P\left( A \right) = \frac{{6 \times 4!}}{{9 \times 8 \times 7 \times 6}} \approx 0,05\).
Câu 2
Lời giải
Chọn B
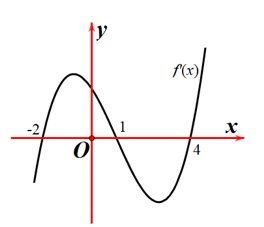
Hàm số đạt cực đại khi \(y = f'\left( x \right)\) đổi dấu từ dương sang âm. Quan sát đồ thị của đạo hàm \(y = f'\left( x \right)\) thì hàm số sẽ đạt cực đại tại \(x = 1\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.