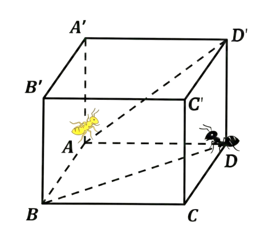
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(20{\rm{ cm}}\). Giả sử hai chú kiến vàng và đen xuất phát cùng một lúc tại các vị trí \(A\) và \(D\), kiến vàng đi thẳng từ \(A\) đến \(D'\) với vận tốc \(2{\rm{ cm/s}}\) và kiến đen đi thẳng từ \(D\) đến \(B\) với vận tốc \(3{\rm{ cm/s}}\). Hỏi khoảng cách ngắn nhất giữa hai chú kiến là bao nhiêu cm? (Kết quả làm tròn đến hàng phần chục).
Quảng cáo
Trả lời:
Đáp án:
Đáp án: \(11,7\)
Chọn hệ trục tọa độ như hình vẽ
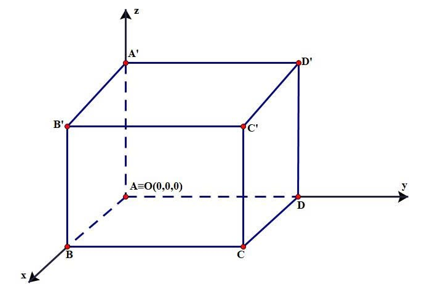
Lúc khó: \(A\left( {0,0,0} \right),B\left( {20,0,0} \right),D\left( {0,20,0} \right),D\prime \left( {0,20,20} \right)\)
- Vectơ chỉ phương của đường thẳng \(AD\prime \) là \(\overrightarrow {AD'} = \left( {0,20,20} \right)\) và độ dài \(\left| {\overrightarrow {AD'} } \right| = 20\sqrt 2 \)
Kiến vàng đi thẳng từ \(A\) đến \(D'\) với vận tốc \(2{\rm{ cm/s}}\)
⇒ Vectơ vận tốc kiến vàng: \({\vec v_1} = \frac{{\overrightarrow {AD'} }}{{\left| {\overrightarrow {AD'} } \right|}}.{v_1} = \left( {0;\sqrt 2 ;\sqrt 2 } \right)\)
- Vectơ chỉ phương đường thẳng \(DB\) là \(\overrightarrow {DB} = \left( {20, - 20,0} \right)\) và độ dài \(\left| {\overrightarrow {DB} } \right| = 20\sqrt 2 \)
Kiến đen đi thẳng từ \(D\) đến \(B\) với vận tốc \(3{\rm{ cm/s}}\).
⇒ Vectơ vận tốc kiến đen: \({\vec v_2} = \frac{{\overrightarrow {BD} }}{{\left| {BD} \right|}}.{v_2} = \left( {\frac{3}{{\sqrt 2 }}, - \frac{3}{{\sqrt 2 }},0} \right)\)
Gọi \(t\) (giây) là thời gian kể từ lúc xuất phát.
* Vị trí kiến vàng tại thời điểm t là \(M\left( t \right) = \left( {0,\sqrt 2 t,\sqrt 2 t} \right)\)
* Vị trí kiến đen tại thời điểm t là \(N\left( t \right) = \left( {\frac{3}{{\sqrt 2 }}t,20 - \frac{3}{{\sqrt 2 }}t,0} \right)\)
Khoảng cách giữa hai chú kiến là \(MN\) và
\(M{N^2}(t){\rm{ }} = {\left( {\frac{3}{{\sqrt 2 }}t} \right)^2} + {\left( {20 - \frac{3}{{\sqrt 2 }}t - \sqrt 2 t} \right)^2} + {(\sqrt 2 t)^2} = 19{t^2} - 100\sqrt 2 t + 400\)
Giá trị nhỏ nhất của \(M{N^2}\) đạt được khi: \(t = \frac{{50\sqrt 2 }}{{19}}\)
Khi đó: \(M{N_{\min }} = \sqrt {\frac{{2600}}{{19}}} \approx 11,7\left( {\;{\rm{cm}}} \right)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: –37.
+ Gọi C: “lấy được 3 bi đỏ từ hộp\[C\]”
\[{B_i}\]: “lấy \[i\]bi đỏ hộp\[B\]”
\({A_i}\): “Lấy \[i\]bi đổ hộp\[A\]”
+ Ta có
\[\begin{array}{l}P\left( C \right) = P\left( {{A_0}} \right)P\left( {{B_1}/{A_0}} \right)P\left( {C/{B_1}} \right) + P\left( {{A_0}} \right)P\left( {{B_2}/{A_0}} \right)P\left( {C/{B_2}} \right) + P\left( {{A_1}} \right)P\left( {{B_1}/{A_1}} \right)P\left( {C/{B_1}} \right) + \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + P\left( {{A_1}} \right)P\left( {{B_2}/{A_1}} \right)P\left( {C/{B_2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = \frac{3}{8}.\frac{{2.3}}{{C_5^2}}.\frac{1}{{C_6^3}} + \frac{3}{8}.\frac{1}{{C_5^2}}.\frac{{C_4^3}}{{C_6^3}} + \frac{5}{8}.\frac{{2.3}}{{C_5^2}}.\frac{1}{{C_6^3}} + \frac{5}{8}.\frac{{C_3^2}}{{C_5^2}}.\frac{{C_4^3}}{{C_6^3}} = \frac{3}{{40}} \Rightarrow a = 3;b = 40.\end{array}\]
Vậy \[a - 40 = - 37\].
Lời giải
Đáp án: 0,88.
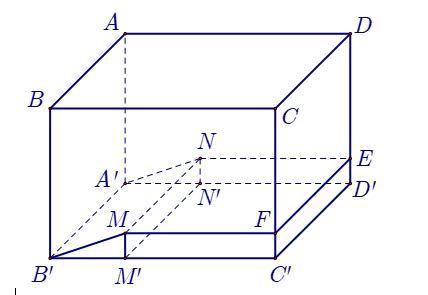
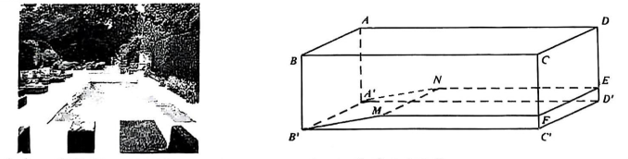
Ta có: \({V_{ABCD.A'B'C'D'}} = AB.AD.AA' = 10.30.2 = 600{\rm{ }}{{\rm{m}}^3}.\)
\(\begin{array}{l}FC' = ED' = 2 - 1,7 = 0,3{\rm{ m}}\\{S_{B'C'FM}} = \frac{{MF + B'C'}}{2}.FC' = \frac{{20 + 30}}{2}.0,3 = 25.0,3 = 7,5{\rm{ }}{{\rm{m}}^2}.\\{V_{B'C'FM.A'D'EN}} = {S_{B'C'FM}}.A'B' = 7,5.10 = 75{\rm{ }}{{\rm{m}}^3}.\end{array}\)
Vậy tỉ số cần tìm là: \(t = \frac{{600 - 75}}{{600}} = \frac{{525}}{{600}} = \frac{7}{8} = 0,875 \approx 0,88.\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.