Một cây cầu bắc qua sông có dạng cung \(OA\) của đồ thị hàm số \(y = 4,8\sin \frac{x}{9}\) và được mô tả trong hệ trục tọa độ với đơn vị trục là mét như hình vẽ. Trục \(Ox\) nằm trên mặt nước sông.
Quảng cáo
Trả lời:
d) Đúng
Ta có phương trình hoành độ giao điểm với trục hoành (\(y = 0\)): \(4,8\sin \left( {\frac{x}{9}} \right) = 0 \Rightarrow \frac{x}{9} = k\pi \).
Tại \(O\), \(x = 0\). Điểm \(A\) ứng với \(k = 1\) (nghiệm dương nhỏ nhất), suy ra \({x_A} = 9\pi \).
Chiều rộng sông: \(OA = 9\pi \approx 28,274\) mét.
Làm tròn đến hàng phần mười: \(28,3\) m.
Kết luận: Đúng.
b) Sai
Đỉnh cầu (điểm cao nhất): Khi \(\sin \left( {\frac{x}{9}} \right) = 1 \Rightarrow {y_{\max }} = 4,8\) mét.
Vậy đỉnh cầu cao \(4,8\)m so với mặt nước.
Kết luận: Sai.
c) Đúng
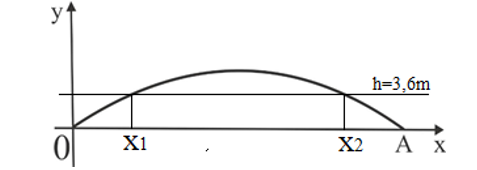
Ta cần tìm độ rộng của phần vòm cầu có độ cao \(y \ge 3,6\).
Giải phương trình:
(với \(\alpha \approx 0,848...\) )
Vị trí 1 (Bên trái): \({x_1} = 9 \cdot \alpha \)
Vị trí 2 (Bên phải): \({x_2} = 9 \cdot (\pi - \alpha )\)
Chiều rộng tối đa cho phép = \({x_2} - {x_1} \approx 20,6415 - 7,632 = 13,0095\) m.
Làm tròn đến hàng phần trăm: 13,01
Kết luận: Đúng
a) Sai
Ta có: muốn xà lan đi lọt thì phải đi vào giữa, và chiều cao của khối hàng hóa mép ngoài cùng (\({x_2}\)) phải nhỏ hơn chiều cao của cầu cũng tại vị trí (\({x_2}\))
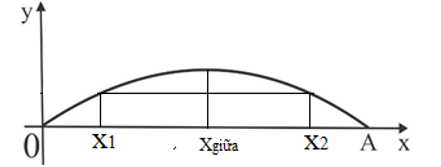
Điểm chính giữa sông (trục đối xứng) có toạ độ: \({x_{giua}} = \frac{{9\pi }}{2} \approx 14,137{\rm{ }}(m)\)
Để sà lan đi qua dễ nhất, người lái tàu phải canh cho sà lan đi chính giữa sông (nơi cầu cao nhất).
Bề rộng sà lan là \(9{\rm{ }}m\). Vì đi chính giữa nên sà lan sẽ nằm về hai phía của tâm, mỗi bên một nửa là 4,5m
Khi sà lan đi qua, phần rủi ro va chạm nhất chính là hai mép ngoài cùng của thùng hàng (vì càng ra xa tâm, cầu càng thấp xuống).
Tọa độ \({x_2}\) của mép sà lan sẽ là: \({x_2} = {x_{m\'e p}} = {x_{giua}} + 4,5 = \frac{{9\pi }}{2} + 4,5\) và độ cao của cầu tại điểm có hoành độ \({x_2} = {x_{m\'e p}} = {x_{giua}} + 4,5 = \frac{{9\pi }}{2} + 4,5\) là\(y = 4,8 \cdot \sin \left( {\frac{{\frac{{9\pi }}{2} + 4,5}}{9}} \right) \approx 4,212{\rm{ }}(m)\).
Vậy chiều cao của khối hàng hóa đó phải nhỏ hơn 4,2 m chứ không phải 4,1m.
Kết luận: Sai
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
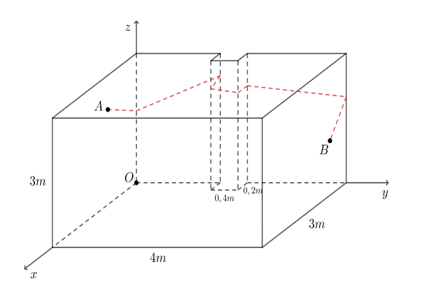
Gọi các đỉnh của đoạn dây điện như ở hình vẽ này:
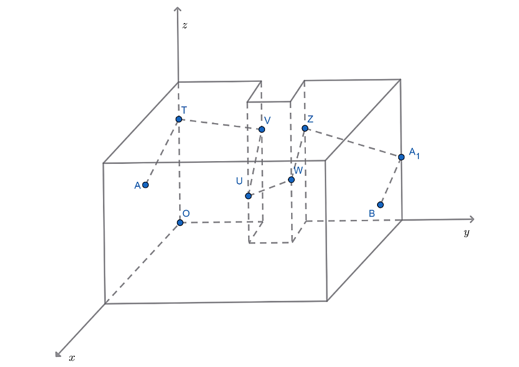
Trải tường chứa \(A\); tường chứa \(B\);các mặt của cột lên mặt phẳng \(Oyz\) ta có hình vẽ sau:
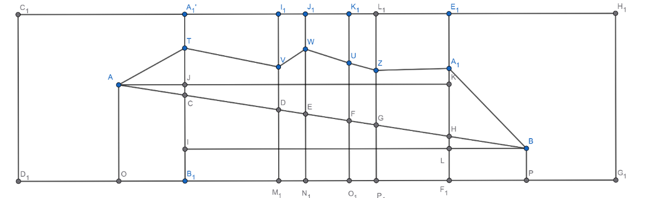
Ta nhận thấy như sau: Khi trải phẳng hình như trên; độ dài của đoạn dây điện vẫn được bảo toàn; đồng thời nhìn vào hình vẽ trên ta thấy được độ dài đoạn dây điện sẽ lớn hơn hoặc bằng độ dài đoạn \(AB\) khi trải hình như trên. Như vậy; ta đi tính độ dài đoạn \(AB\) khi trai hình như trên.
Lấy \(O'\) là hình chiếu của \(A\) lên \({B_1}{D_1}.\) \(P\) là hình chiếu của \(B\) lên \({F_1}{G_1}.\)
Khi đó \(AO'\) ở hình vẽ trên cũng chính bằng khoảng cách từ điểm \(A\) của đề lên \(Oy\) và nó cũng bằng \(2,5\). Tương tự \(BP = 1\).
\(O'{B_1}\) sẽ bằng khoảng cách từ \(A\) đến \(Oz\) và bằng \(1\). Tương tự \({F_1}P = 0,5.\)
Ta có độ dài \({B_1}{F_1} = {A_1}{I_1} + {I_1}{J_1} + {J_1}{K_1} + {K_1}{L_1} + {L_1}{E_1} = 4 + 0,2.2 = 4,4 \Rightarrow O'P = 1,5 + 4,4 = 5,9\).
Do đó nên theo định lý Pytago ta có \(AB = \sqrt {O'{P^2} + {{\left( {AO' - BP} \right)}^2}} \approx 6,09\).
Vậy nên độ dài đoạn dây điện tối thiểu xấp xỉ \(6,09\;\)m.
Lời giải
Đáp số: \(0,66\).
Số cách chọn của Hải là: \(n(H) = C_9^3 = 84\).
Số cách chọn của Sơn là: \(n(S) = C_8^3 = 56\).
Do đó: \(n(\Omega ) = 84 \times 56 = 4704\).
Ta thấy nếu số của Hải lớn hơn số của Sơn thì xảy ra trong hai trường hợp sau:
*Trường hợp 1: Hải chọn được quả bóng số 9
Nếu Hải chọn được bóng số 9, số của Hải chắc chắn bắt đầu bằng chữ số 9 (dạng 9bc)
Do đó, hễ Hải có số 9 là Hải chắc chắn thắng.
Số cách Hải chọn có số 9 là: \(1 \times C_8^2 = 28\) cách.
Với mỗi cách này, Sơn có thể chọn bất kỳ trong 56 cách.
Số kết quả thuận lợi ở TH1: \(28 \times 56 = 1568\).
*Trường hợp 2: Hải không chọn được quả bóng số 9
Lúc này, cả Hải và Sơn đều chọn 3 bóng từ cùng một tập số \(\{ 1,2, \ldots ,8\} \).
Số cặp kết quả trong trường hợp này là: \(C_8^3 \times C_8^3 = 56 \times 56 = 3136\).
Vì tập số của hai bạn là như nhau, nên theo tính đối xứng, số trường hợp Hải thắng (\(X > Y\)) sẽ bằng số trường hợp Sơn thắng (\(X < Y\)).
Số trường hợp hòa (\(X = Y\)) xảy ra khi hai bạn chọn trùng bộ 3 quả bóng: có 56 trường hợp.
Số kết quả Hải thắng (Sơn thua) ở TH2 là: \({n_2} = \frac{{3136 - 56}}{2} = 1540\)
Tổng số trường hợp thuận lợi để Sơn thua là: \(n(A) = 1568 + 1540 = 3108\)
Xác suất để Sơn thua là: \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{3108}}{{4704}} \approx 0,66\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.