Cho tam giác \(ABC\) cân tại \(A\). Đường trung tuyến \(BD\) và \(CE\) cắt nhau tại \(G\).

a) Chứng minh \(\Delta DGE\) cân;

b) Chứng minh \(BD + CE > \frac{3}{2}BC\).

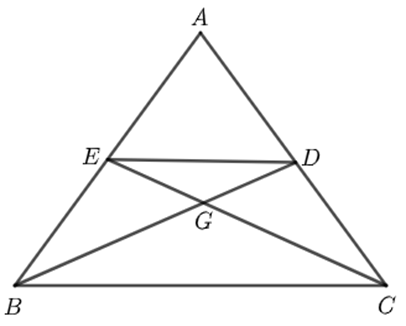
a) Vì tam giác \(ABC\) cân tại \(A\) nên \(AB = AC\)(1).

Vì \(BD\); \(CE\) là đường trung tuyến nên \(D\) là trung điểm của \(AC\) và \(E\) là trung điểm của \(AB\).

Do đó, \(AE = EB = \frac{1}{2}AB;\,\,AD = DC = \frac{1}{2}AC\) (2)

Từ (1) và (2) suy ra \(AE = EB = AD = DC\).

Xét \(\Delta BEC\) và \(\Delta CDB\) có:

\(BE = DC\) (chứng minh trên)

Cạnh \(BC\) chung

\(\widehat {EBC} = \widehat {DCB}\) (do \(\Delta ABC\) cân tại \(A\))

Do đó, \(\Delta BEC = \Delta CDB\) (g.c.g)

Suy ra \(BD = CE\) (hai cạnh tương ứng) và \(\widehat {ECB} = \widehat {DBC}\) (hai góc tương ứng)

Xét tam giác \(BGC\) có: \(\widehat {ECB} = \widehat {DBC}\) hay \(\widehat {GCB} = \widehat {GBC}\).

Do đó \(\Delta BGC\) cân tại \(G\).

Suy ra \(GB = GC\) (tính chất tam giác cân)

Ta có: \(BD = BG + GD;\,\,CE = CG + GE\).

Mà \(BD = EC;\,\,BG = GC\) nên \(GE = GD\).

Xét tam giác \(EGD\) có: \(GE = GD\) nên \(\Delta EGD\) cân tại \(G\).

b) Xét tam giác \(BGC\) có:

\(BG + GC > BC\) (bất đẳng thức tam giác) (*)

Vì hai đường trung tuyến \(BD;CE\) cắt nhau tại \(G\) nên \(G\) là trọng tâm tam giác \(ABC\).

Ta có: \[BG = \frac{2}{3}BD;\,\,CG = \frac{2}{3}CE\] (**)

Thay (**) vào (*) ta được: \(BG + CG = \frac{2}{3}BD + \frac{2}{3}CE > BC\) hay \(\frac{2}{3}\left( {BD + CE} \right) > BC\).

Suy ra \(BD + CE > \frac{3}{2}BC\) (đpcm).