Phòng luyện đề thi giữa kì 1 năm học 2026-2027 tất cả các môn lớp 1-12

✕

Giảm 50% Kích hoạt VIP

Kích hoạt VIP

Tạo VIP

Câu hỏi:

17/04/2020 5,186

Trong không gian với hệ tọa độ Oxyz, cho hình chóp $S . A B C D$ với $S (1; - 1; 6), A (1; 2; 3), B (3; 1; 2), D (2; 3; 4)$ . Gọi I là tâm mặt cầu (S) ngoại tiếp hình chóp. Tính khoảng cách d từ I đến mặt phẳng (SAD)

A. $d = \frac{\sqrt{6}}{2}$

B. $d = \frac{\sqrt{21}}{2}$

C. $d = \frac{3 \sqrt{3}}{2}$

D. $d = \frac{\sqrt{3}}{2}$

Xem lời giải

Câu hỏi trong đề: Đề thi thử THPTGQ môn Toán cực cực hay có lời giải chi tiết !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn đáp án A

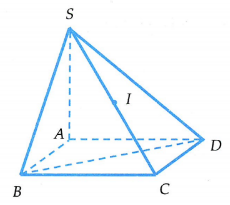
Lấy điểm C trong mặt phẳng (ABD) sao cho ABCD là hình chữ nhật

Do vậy, tâm mặt cầu ngoại tiếp hình chóp là trung điểm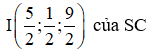

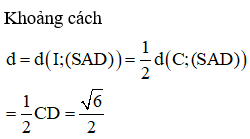
Cách 2: Gọi I(a;b;c) là tâm mặt cầu ngoại tiếp hình chóp là trung điểm S.ABCD. Ta có:

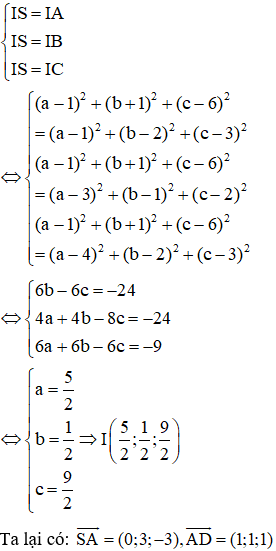
STUDY TIP

Khi xác định tâm mặt cầu ngoại tiếp hình chop hoặc lăng trụ ta có thể làm theo hai hường:

+ Hướng 1: Dùng điều kiện tâm cách đều các đỉnh đi đến giải hệ phương trình

+ Hướng 2: Dựa vào tính đặc biệt của hình như: Hình chop đều, hình chop có các đỉnh cùng nhìn một cạnh dưới một góc vuông

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chóp S.ABC có tam giác ABC vuông tại B, SA vuông góc với mặt phẳng $(A B C), S A = 5, A B = 3, B C = 4$ . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC

A. $R = \frac{5 \sqrt{2}}{2}$

B. $R = \frac{5 \sqrt{2}}{3}$

C. $R = \frac{5 \sqrt{3}}{3}$

D. $R = \frac{5 \sqrt{3}}{2}$

Lời giải

Chọn đáp án C

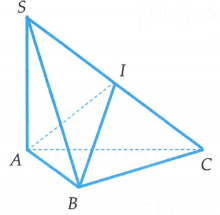
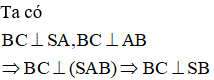
Vậy hai điểm cùng nhìn cạnh dưới một góc vuông. Điều đó chứng tỏ SC là đường kính của mặt cầu ngoại tiếp hình chóp. Do đó bán kính

Câu 2

Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành tâm O; mặt phẳng $(S A C)$ vuông góc với mặt phẳng $(S B D)$ . Biết khoảng cách từ O đến mặt phẳng $(S A B), (S B C), (S C D)$ lần lượt là 1;2; $\sqrt{5}$ . Tính khảng cách d từ O đến mặt phẳng $(S A D)$

A. $d = \sqrt{\frac{20}{19}}$

B. $d = \sqrt{\frac{19}{20}}$

C. $d = \sqrt{2}$

D. $d = \frac{\sqrt{2}}{2}$

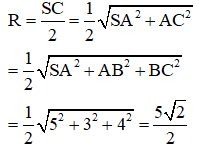
Lời giải

Chọn đáp án A

Cách 1:

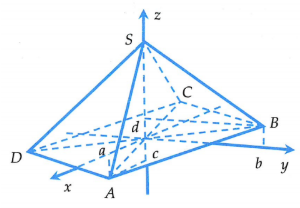
Lấy mặt phẳng $(α)$ vuông góc với SO cắt (SAC), (SBD) theo các giao tuyến x’Ox, y’Oy.

Chọn hệ tọa độ Oxyz sao cho tia Oz trùng với tia OS

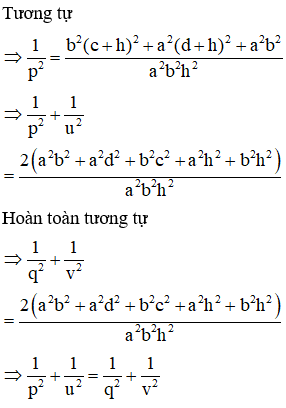
Cách 2:

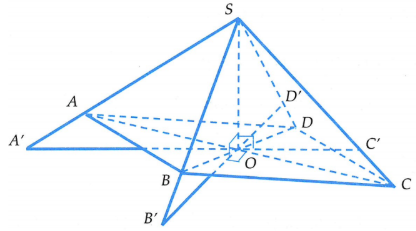
Trong mặt phẳng (SAC) dựng đường thẳng qua O vuông góc với đường thẳng SO cắt hai đường thẳng SA, SC lần lượt tại A’, C’

Trong mặt phẳng (SBD) dựng đường thẳng qua O vuông góc với đường thẳng SO cắt hai đường thẳng SB, SD lần lượt tại B’, D’

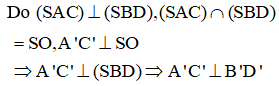
Khi đó tứ diện OSA’B’ có OS, OA’, OB’ đôi một vuông góc nên ta chứng minh được

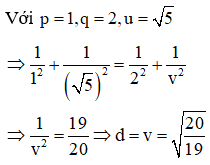
Câu 3

Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc $B_{1}$ , đựng cao Sao vàng và đựng “Quy sâm đại bổ hoàn”. Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau
- Cách thứ nhất cắt được 3 hộp $B_{1}$ , một hộp cao Sao vàng và 6 hộp Quy sâm
- Cách thứ hai cắt được 2 hộp $B_{1}$ , 3 hộp cao Sao vàng và 1 hộp Quy sâm. Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp $B_{1}$ tối thiểu là 900 hộp, số hộp cao Sao vàng tối thiểu là 1000 hộp. Cần phương án sao cho tổng số tấm bìa phải dùng là ít nhất?

A. Cắt theo cách một $x - 2 < 0$ tấm, cắt theo cách hai 300 tấm

B. Cắt theo cách một 150 tấm, cắt theo cách hai 100 tấm

C. Cắt theo cách một 50 tấm, cắt theo cách hai 300 tấm

D. Cắt theo cách một 100 tấm, cắt theo cách hai 200 tấm

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tứ diện ABCD. Gọi M là trung điểm của AB. Cắt tứ diện ABCD bởi mặt phẳng đi qua M và song song với BC và AD, thiết diện thu được là hình gì?

A. Tam giác đều

B. Tam giác vuông

C. Hình bình hành

D. Ngũ giác

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một gia đình cần ít nhất 900 đoen vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilogram thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogram thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền của một kg thịt bò là 160 nghìn đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x, y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính $x^{2} + y^{2}$

A. $x^{2} + y^{2} = 1, 3$

B. $x^{2} + y^{2} = 2, 6$

C. $x^{2} + y^{2} = 1, 09$

D. $x^{2} + y^{2} = 0, 58$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Giá trị tham số thực k nào sau đây để đồ thị hàm số $y = x^{3} - 3 k x^{2} + 4$ cắt trục hoành tại ba điểm phân biệt

A. -1 < k < 1

B. k > 1

C. k < 1

D. $k \geq 1$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Khóa học 1 - 12

THPT

THCS

Phòng luyện đề

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ô Ôn vào 10

Ôn vào 6

Ô Ôn vào 6

Tài liệu

THPT

THCS

Tin Tuyển Sinh