Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có . Hỏi có bao nhiêu điểm (với x, y, z nguyên) nằm trong tứ diện.
A. 4
B. 1
C. 10
D. 7
Quảng cáo
Trả lời:
Đáp án A.
Cách 1:

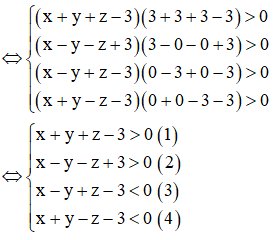
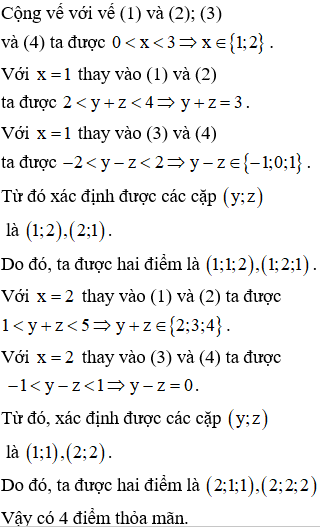

Do các mặt của tứ diện có diện tích bằng nhau nên
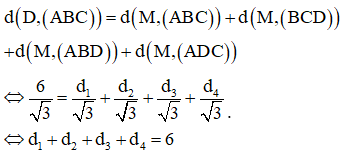

Kiểm tra các trường hợp chỉ có bốn điểm thỏa mãn.

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. một số chẵn lớn hơn hoặc bằng 6.
B. một số chẵn lớn hơn hoặc bằng 4
C. một số lẻ lớn hơn hoặc bằng 7
D. một số lẻ lớn hơn hoặc bằng 5.
Lời giải
Đáp án A.
Giả sử đa giá đáy của hình chóp có n cạnh . Khi đó, đa giác đáy có n đỉnh, kết hợp các đỉnh đó với đỉnh của hình chóp ta sẽ có thêm n cạnh bên.
Vậy số cạnh của hình chóp là
Câu 2
A. 922 756 000 đồng.
B. 832 765 000 đồng.
C. 918 165 000 đồng.
D. 926 281 000 đồng
Lời giải
Đáp án A.


Gọi B là số tiền của người đó trong tài khoản tiết kiệm đến hết tháng 12 năm 2020. Khi đó n = 24
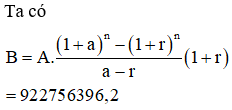
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 44.000 đ.
B. 43.000đ.
C. 42.000đ.
D. 41.000 đ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 2a + b = 2
B. 2a + b = 0
C. 2a + b = -1
D. 2a + b = 1
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.