Câu hỏi:
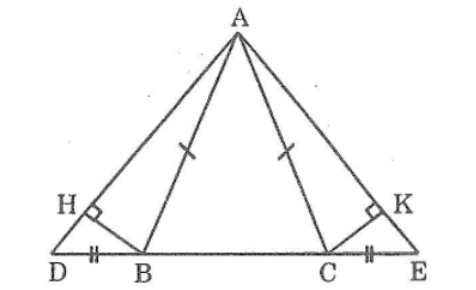
13/07/2024 16,782Cho tam giác ABC cân tại A. Trên tia đối của tai BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Kẻ BH vuông với AD, kẻ CK vuông góc với AE. Chứng minh rằng: BH = CK
Câu hỏi trong đề: Sách bài tập Toán 7 Tập 1 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì ΔABC cân tại A nên∠(ABC) =∠(ACB) (tính chất tam giác cân)
Ta có: ∠(ABC) +∠(ABD) =180o(hai góc kề bù)
∠(ACB) +∠(ACE) =180o(hai góc kề bù)
Suy ra: ∠(ABD) =∠(ACE)
Xét ΔABD và ΔACE, ta có:
AB = AC (gt)
∠(ABD) =∠(ACE) (chứng minh trên)
BD=CE (gt)
Suy ra: ΔABD= ΔACE (c.g.c)
⇒∠D =∠E (hai góc tương ứng)
Xét hai tam giác vuông ΔBHD và ΔCKE, ta có:
∠(BHD) =∠(CKE) = 90º
BD=CE (gt)
∠D =∠E (chứng minh trên)
Suy ra: ΔBHD= ΔCKE (cạnh huyền – góc nhọn)
Suy ra: BH = CK (hai cạnh tương ứng)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
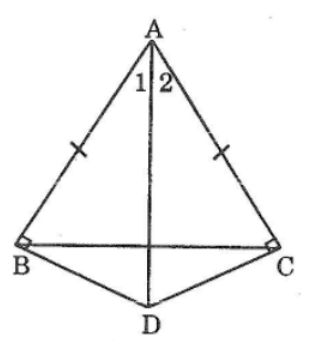
Xét hai tam giác vuông ABD và ACD, ta có:
∠(ABD) =∠(ACD) =90o
Cạnh huyền AD chung
AB = AC (giả thiết)
⇒ ΔABD= ΔACD (cạnh huyền, cạnh góc vuông)
Suy ra: ∠(A1 ) =∠(A2) (hai góc tương ứng)
Suy ra AD là tia phân giác góc A
Lời giải
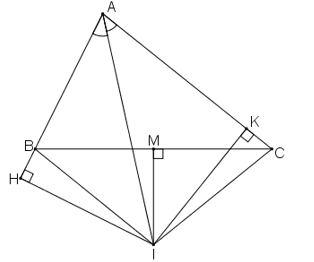
Gọi đường trung trực của BC cắt BC tại M.
Xét ΔBMI và ΔCMI, ta có:
∠(BMI) = ∠(CMI) = 90o (gt)
BM = CM ( vì M là trung điểm của BC )
MI cạnh chung
Suy ra: ΔBMI = ΔCMI(c.g.c)
Suy ra: IB = IC ( hai cạnh tương ứng)
Xét hai tam giác vuông ΔIHA và ΔIKA, ta có:
∠(HAI) = ∠(KAI) ( vì AI là tia phân giác của góc BAC).
∠(IHA) = ∠(IKA) = 90o
AI cạnh huyền chung
Suy ra: ΔIHA = ΔIKA(cạnh huyền góc nhọn)
Suy ra: IH = IK (hai cạnh tương ứng)
Xét hai tam giác vuông ΔIHB và ΔIKC, ta có:
IB = IC ( chứng minh trên )
∠(IHB) =∠(IKC) =90o
IH = IK (chứng minh trên)
Suy ra: ΔIHB = ΔIKC(cạnh huyền.cạnh góc vuông)
Suy ra: BH = CK(hai cạnh tương ứng)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
Đề thi giữa học kì 2 Toán 7 KNTT - Đề 01 có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận