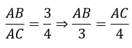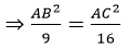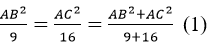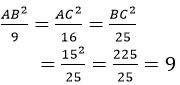Câu hỏi trong đề: Sách bài tập Toán 7 Tập 1 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
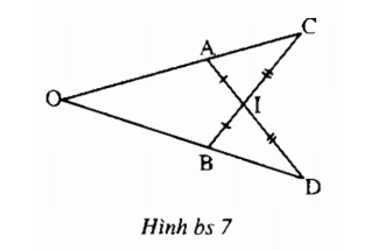
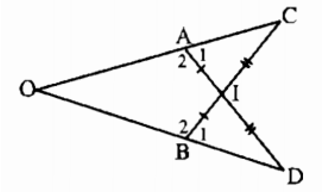
+) Xét ∆AIC và ∆BID có:
AI = BI (giả thiết)
∠AIC = ∠BID ( hai góc đối đỉnh).
IC = ID ( giả thiết)
Suy ra: ∆AIC = ∆BID (c.g.c)
Suy ra: ∠C = ∠D; ∠A1 = ∠B1 (1)
+) Lại có: ∠A1 + ∠A2 = 180º (hai góc kề bù)
Và ∠B1 + ∠B2 = 180º (hai góc kề bù)
Suy ra: ∠A2 = ∠B2
+) Xét tam giác OAD và ∆ OBC có:
∠A2 = ∠B2 (chứng minh trên)
AD = BC (vì AI + ID = BI + IC)
∠D = ∠C (chứng minh trên)
Suy ra: ∆OAD = ∆ OBC (g.c.g)
Suy ra: OA = OB (hai cạnh tương ứng).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Theo đề bài ta có:
Theo tính chất dãy tỉ số bằng mhau ta có:
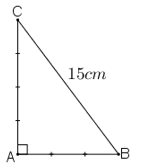
tam giác ABC vuông tại A
Áp dụng định lí pitago vào tam giác ABC ta có:
BC2 = AB2 + AC2 (2)
Từ (1) và (2) suy ra:
AB2 = 9. 9 = 81 ⇒ AB = 9 cm (vì AB > 0)
AC2 = 16. 9 = 144 ⇒ AC = 12 cm (vì AC > 0)
Lời giải
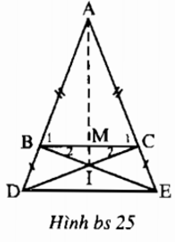
+)Theo giả thiết ta có: AB = AC và BD = CE nên:
AB + BD = AC + CE hay AD = AE.
+) Xét ΔABE và ΔACD có:
AB = AC (gt)
∠A chung
AE = AD (chứng minh trên)
⇒ ΔABE = ΔACD (c.g.c)
⇒ BE = CD (2 cạnh tương ứng) (1)
và ∠ABE = ∠ACD (2 góc tương ứng) (2)
Tam giác ABC cân nên ∠B1 = ∠C1. (3)
Từ (2) và (3) ⇒ ∠ABE - ∠B1 = ∠ACD - ∠C1, tức là ∠B2 = ∠C2.
⇒ ΔBIC cân tại I ⇒ IB = IC. (4)
Từ (1) và (4) suy ra BE - IB = CD – IC, tức là IE = ID.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2