Từ 9 học sinh gồm 4 học sinh giỏi, 3 học sinh khác, 2 học sinh trung bình, giáo viên muốn thành lập 3 nhóm làm 3 bài tập lớn khác nhau, mỗi nhóm 3 học sinh. Tính xác suất để nhóm nào cũng có học sinh giỏi và học sinh khá.
A.
B.
C.
D.
Câu hỏi trong đề: ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN !!
Quảng cáo
Trả lời:
Chọn C.
Số phần tử của không gian mẫu là
Gọi X là biến cố “nhóm nào cũng có học sinh giỏi và học sinh khá”
Khi đó, ta xét các chia nhóm như sau:
· N1: 2 học sinh giỏi, 1 học sinh khá.
· N2: 1 học sinh giỏi, 1 học sinh khá và
· 1 học sinh trung bình.
· N3: 1 học sing giỏi, 1 học sinh khá
· và 1 học sinh trung bình.
Suy ra có cách chia
Vậy xác suất cần tính là
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

Câu 2
A. 10 N.
B. 5 N.
C. 20 N.
D. 20N.
Lời giải

Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
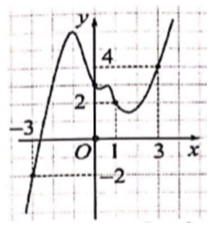
A. Phương trình g(x)=0 có đúng hai nghiệm thuộc [-3;3].
B. Phương trình g(x)=0 có đúng một nghiệm thuộc [-3;3].
C. Phương trình g(x)=0 không có nghiệm thuộc [-3;3].
D. Phương trình g(x)=0 có đúng ba nghiệm thuộc [-3;3].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 8ln2.
B. 3ln2
C. 6ln2
D. 4ln2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. M(-4;-4;-4).
B. M(1;2;3).
C. M(2;4;6).
D. M(4;4;4).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.