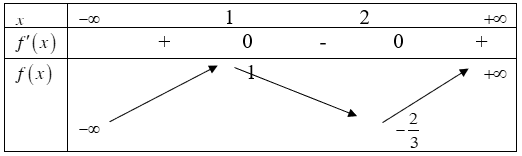
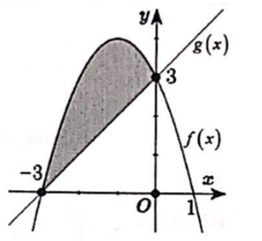
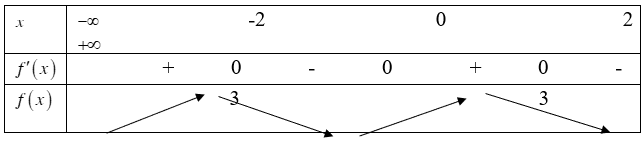
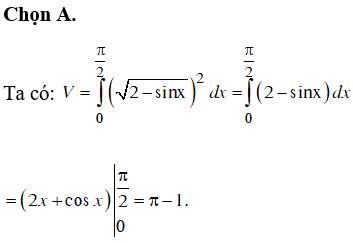ĐỀ THI THỬ THPT QUỐC GIA NĂM HỌC 2019 MÔN TOÁN (Đề số 14)
30 người thi tuần này 4.6 26.4 K lượt thi 50 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm trường THPT Hà Tĩnh có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Phú Thọ có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Đồng Hỷ (Thái Nguyên) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Trần Phú (Hải Phòng) lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Lê Quý Đôn (Hà Nội) lần 01 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Khuyến (TP.HCM) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Cửa Lò (Nghệ An) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Hạ Long lần 01 có đáp án
Danh sách câu hỏi:
Lời giải

Lời giải
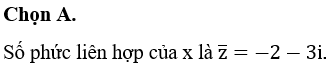
Câu 3
A. x = 0.
B. x = -1.
C. y = 0.
D. x = 1
Lời giải

Câu 4
A. m =
B. m = 0.
C. m= - hoặc m= 0.
D. m= hoặc m= 0.
Lời giải
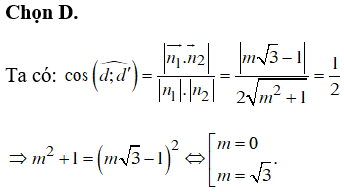
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 10 N.
B. 5 N.
C. 20 N.
D. 20N.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. M(-4;-4;-4).
B. M(1;2;3).
C. M(2;4;6).
D. M(4;4;4).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. 24.
B. 12.
C. 48.
D. 86.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. 10x+6y+15z-90= 0
B. 10x+6y+15z-60= 0
C.3x+5y+2z-60= 0
D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. 1
B. 2
C. 3.
D. 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. A(3;9;0) và B(0;0;15)
B. A(6;15;0) và B(0;0;24).
C. A(7;16;0) và B(0;0;25).
D. A(5;14;0) và B(0;0;23).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. I=
B. I=
C. I= -
D. I= 147.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A.
B. (-2;2).
C. (-2;0).
D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. z có phần thực và phần ảo đều dương.
B. z có phần thực và phần ảo đều âm
C. z có phần thực dương và phần ảo âm
D. z có phần thực âm và phần ảo dương.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
A. x+y-2=0.
B. x-y+2=0.
C. x+y-1=0.
D. x+y+1=0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
A. x+y-2=0.
B. x-y+2=0.
C. x+y-1=0.
D. x+y+1=0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
A. P = 4.
B. P = 0
C. P = 2
D. P = 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
A. P=4
B. P=2
C. P=5+3
D. P=34+3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 38
A.
B.
C. m> 2 hoặc m< -2
D. m> 2 hoặc m< -3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 39
A. -10.
B. 10
C. 12
D. -20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 41
A. 200
B. 101
C. 100
D. 201.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 42
A. 108 số.
B. 72 số.
C. 423 số
D. 216 số
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 43
A. 8ln2.
B. 3ln2
C. 6ln2
D. 4ln2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 46
A. 29.
B. 1369/36.
C. 30.
D. 505/36
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
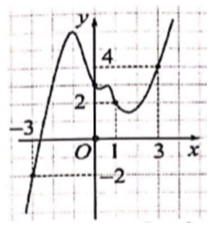
Câu 50
A. Phương trình g(x)=0 có đúng hai nghiệm thuộc [-3;3].
B. Phương trình g(x)=0 có đúng một nghiệm thuộc [-3;3].
C. Phương trình g(x)=0 không có nghiệm thuộc [-3;3].
D. Phương trình g(x)=0 có đúng ba nghiệm thuộc [-3;3].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.