Câu hỏi:
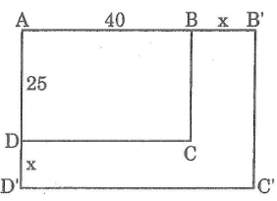
11/07/2024 4,840Một hình chữ nhật có kích thước là 25cm và 40cm. Người ta tăng mỗi kích thước của hình chữ nhật thêm x cm. Gọi S và P theo thứ tự là diện tích và chu vi hình chữ nhật mới tính theo x. Hỏi rằng các đại lượng S và P có phải là hàm số bậc nhất của x không? Vì sao?
Câu hỏi trong đề: Giải Sách Bài Tập Toán 9 Tập 1 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Sau khi tăng kích thước của mỗi chiều, ta được hình chữ nhật A’B’C’D’ có chiều dài A’B’ = (40 + x) cm, chiều rộng B’C’ = (25 + x) cm.
Diện tích hình chữ nhật mới:
S = (40 + x)(25 + x) = 1000 + 65x +
S không phải là hàm số bậc nhất đối với x vì có bậc của biến số x là bậc hai.
Chu vi hình chữ nhật mới:
P = 2.[(40 + x) + (25 + x)] = 4x + 130
P là hàm số bậc nhất đối với x có hệ số a = 4, hệ số b = 130.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hàm số bậc nhất y = ax + b (a ≠ 0) trên tập số thực R
Với hai số và thuộc R và < , ta có:
= + b
= + b
– = (a + b) – (a + b) = a( – ) (1)
*Trường hợp a > 0:
Ta có: < suy ra: – > 0 (2)
Từ (1) và (2) suy ra: – = a( – ) > 0 ⇒ >
Vậy hàm số đồng biến khi a > 0
*Trường hợp a < 0:
Ta có: < suy ra: – > 0 (3)
Từ (1) và (3) suy ra: – = a( – ) < 0 ⇒ <
Vậy hàm số nghịch biến khi a < 0
Lời giải
Hàm số y = (3 - )x + 1 có hệ số a = 3 - , hệ số b = 1
Ta có: a = 3 - > 0 nên hàm số đồng biến trên R
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo